Un triangolo rettangolo è probabilmente la figura geometrica più importante in assoluto! Proprio i segreti nel passato furono la base per lo sviluppo di parti completamente nuove della geometria e della trigonometria. Questi dati indicano che ogni appassionato di matematica deve sapere tutto su questo tipo di triangolo e sulle leggi che si applicano ad esso. In questo post presenteremo i dati di base e le formule utilizzate per comprendere appieno un dato triangolo. Di seguito puoi vedere come vengono calcolati il perimetro e l’area di questo tipo di triangolo se si conoscono le lunghezze dei suoi lati.
Ti consigliamo di continuare a leggere qui sotto!
Informazioni di base
Un triangolo rettangolo è qualsiasi triangolo il cui angolo misura esattamente 90 gradi. Gli altri due angoli del triangolo rettangolo sono acuti e anche la loro somma è 90 gradi.
Il lato opposto all’angolo retto (angolo di 90 gradi) è il più lungo in questo tipo di triangolo ed è chiamato ipotenusa! Gli altri due lati si chiamano gambe!
Uno dei teoremi più importanti della matematica è valido solo per questo tipo di triangolo (il teorema di Pitagora – clicca sul testo colorato per vedere maggiori informazioni su questo teorema) e recita: Il quadrato dell’ipotenusa in un triangolo rettangolo è sempre uguale alla somma dei quadrati delle gambe. Questo teorema è la base della geometria e della trigonometria moderne. Molti problemi e problemi geometrici possono essere risolti utilizzando questo teorema.
Come calcolare il perimetro di un triangolo rettangolo
Il perimetro di un triangolo rettangolo si calcola utilizzando la formula che si applica a tutti gli altri tipi di triangoli. La formula per calcolare il perimetro è riportata nella figura seguente!
Per determinare il perimetro di questo tipo di triangolo è sufficiente calcolare la somma delle lunghezze di tutti i suoi lati.
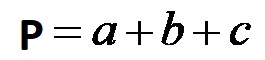
Di seguito puoi vedere in un esempio concreto come determinare il perimetro di questa figura geometrica.
Esempio 1. Calcola il perimetro con ipotenusa 29 centimetri, se i suoi cateti hanno lunghezze di 20 e 21 centimetri!
Per prima cosa inseriamo i dati forniti nella formula per calcolare il perimetro di questo tipo di triangolo. Dopo aver inserito otteniamo l’espressione:
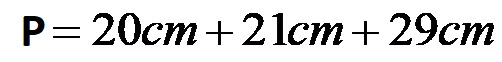
Alla fine basterà calcolare la somma totale delle tre lunghezze, dopodiché si otterrà la soluzione finale:
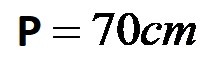
Il perimetro è 70 centimetri.
Continua a leggere per vedere come calcolare l’area di questo tipo di triangolo!
Area di un triangolo rettangolo
L’area di un triangolo rettangolo si calcola in modo molto più semplice rispetto a qualsiasi altro tipo di triangolo. La formula per calcolare l’area di un triangolo rettangolo è la seguente:
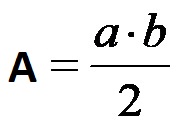
L’area di un triangolo rettangolo è pari al semiprodotto dei suoi cateti!
Vediamo in un esempio concreto come determinare l’area di questo tipo di triangolo!
Esempio 2. Calcola l’area se è noto che la lunghezza delle sue gambe è 14 e 3 decimetri!
Innanzitutto, inseriamo i valori indicati nella formula per calcolare l’area di un triangolo rettangolo. Si ottiene la seguente espressione!
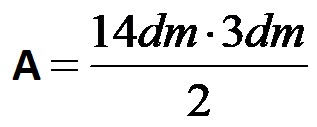
Ora, nel passaggio successivo, viene calcolato il prodotto delle gambe.
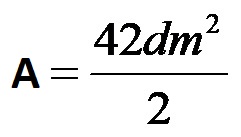
Infine dividiamo per il numero 2, dopodiché otteniamo la soluzione finale, ovvero l’area del triangolo rettangolo.
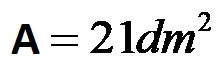
L’area e 21 decimetri quadrati!
Come probabilmente avrai già notato dai due esempi risolti sopra in questa pagina web, calcolare il perimetro e l’area di un triangolo rettangolo non è affatto difficile. Al contrario, con i dati reali sulla lunghezza dei lati di questo tipo di triangolo è molto semplice calcolare il perimetro e l’area di questa figura geometrica.
Video Problemi Matematici
Il materiale video di seguito contiene molti problemi matematici risolti in cui il perimetro e l’area di un triangolo rettangolo vengono determinati utilizzando le formule di calcolo di cui sopra. Ti consigliamo di guardare parte del video e ricordare la procedura per determinare il perimetro e l’area di questo tipo di triangolo.
*Raccomandazione! Guardati attorno e individua dei triangoli rettangoli! Sono tutti intorno a te, vero?
Buona fortuna!
Tags: Area, Esempi, Esempio, Formula, Perimetro, Problema, Rettanglolo, Triangolo

 Attendere prego...
Attendere prego...