Quali sono le caratteristiche più importanti di un triangolo isoscele? Quali sono le formule matematiche più importanti che possono essere utilizzate per calcolare determinate caratteristiche e valori di un triangolo isoscele? Troverai le risposte a queste domande se continui a leggere questo testo. Di seguito puoi trovare le formule per calcolare il perimetro e l’area, nonché esempi risolti di problemi matematici in cui vengono determinati il perimetro e l’area di questo tipo di triangolo. Oltre agli esempi che trovi direttamente in questo testo, in fondo al testo puoi accedere ad un materiale video che contiene un numero enorme di esempi risolti!
Informazioni importanti
Un triangolo isoscele è un triangolo che ha solo due lati uguali. In questo tipo di triangolo il terzo lato è sempre di lunghezza diversa rispetto ai due lati uguali. I due lati uguali di questo tipo di triangolo si chiamano cateti, mentre il terzo lato si chiama base. La base è sempre indicata con la lettera latina minuscola a, mentre entrambi i bracci sono indicati con la lettera latina minuscola b a causa della loro uguale lunghezza!
In un triangolo isoscele si possono rappresentare tre altezze, di cui due uguali tra loro (le due altezze corrispondono ai cateti del triangolo isoscele). Utilizzando queste altezze e utilizzando formule matematiche aggiuntive, è facile determinare valori sconosciuti che sono importanti e caratterizzano di questo tipo di triangolo!
Perimetro
Il perimetro di un triangolo isoscele è la somma delle lunghezze di tutti i suoi lati. Quando si formula la formula di calcolo, è importante tenere conto del fatto che di questo tipo di triangolo ha due lati uguali. La formula è riportata nell’immagine qui sotto!
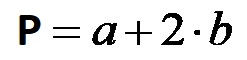
Per calcolare il perimetro è sufficiente conoscere la lunghezza della base e la lunghezza di una delle gambe!
Vedi l’esempio risolto qui sotto!
Esempio 1. Calcola il perimetro che ha la base di 12 centimetri e il lato lungo 20 centimetri!
Inserendo i valori indicati nella formula sopra, si ottiene la seguente espressione matematica:
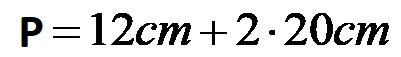
Per prima cosa calcoliamo il prodotto del numero 2 e la lunghezza della gamba.
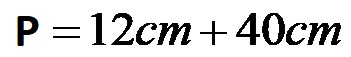
Infine, aggiungiamo i numeri risultanti nell’ultima espressione!
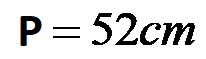
Il perimetro di 52 centimetri!
Sei interessato a leggere ulteriori informazioni su un triangolo equilatero?
Continua a leggere qui sotto per vedere come calcolare l’area di questo tipo di triangolo!
Area di un triangolo isoscele
L’area di un triangolo isoscele può essere facilmente calcolata conoscendo la lunghezza di uno qualsiasi dei suoi lati e l’altezza corrispondente! La formula per calcolare l’area di questo tipo di triangolo è:
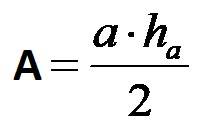
Diamo un’occhiata a un esempio in cui viene calcolata l’area di questa figura geometrica!
Esempio 2. Calcola l’area con base di 4 metri, se la sua altezza corrispondente ha una lunghezza di 5 metri!
Nella prima fase, inseriamo i dati forniti nella formula per determinare l’area di un triangolo isoscele.
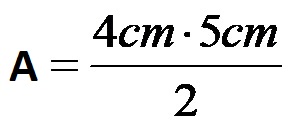
Adesso calcoliamo il prodotto della base per la sua altezza!
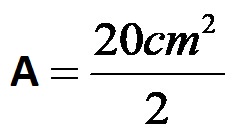
Alla fine dividiamo per il numero 2!
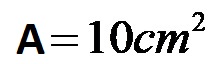
L’area di 10 metri quadrati!
*Se l’altezza di un triangolo isoscele non è nota, può essere calcolata utilizzando il teorema di Pitagora, perché l’altezza ridotta alla base di un triangolo isoscele divide questo tipo di triangolo in due triangoli rettangoli identici!
Esempi video
Il materiale video qui sotto ti offre la possibilità di vedere altri esempi risolti di problemi di matematica con il calcolo del perimetro e dell’area di un triangolo isoscele, se pensi di averne bisogno!
Tags: Area, Esempi, Esempio, Formula, Isoscele, Perimetro, Problema, Triangolo

 Attendere prego...
Attendere prego...