Sai cosa mostra il teorema di Pitagora? Sapete che uno dei teoremi più famosi, più importanti e più utilizzati in geometria è il teorema di Pitagora? Qui in questa pagina qui sotto puoi leggere molte informazioni su questo famoso teorema matematico, la sua definizione, il suo significato e l’applicazione concreta nella risoluzione di compiti matematici nel campo della geometria.
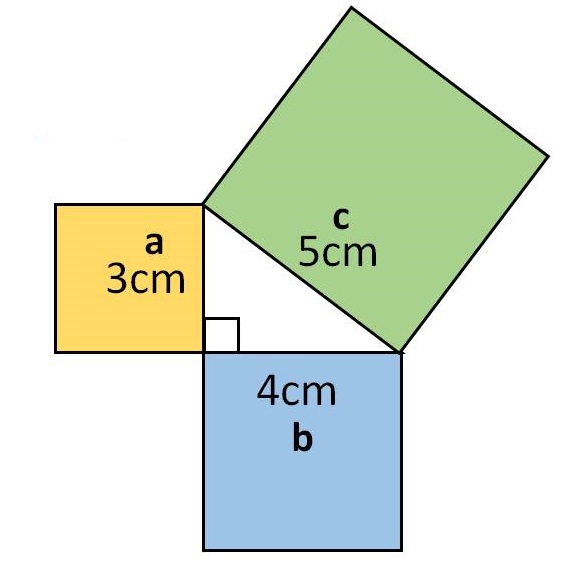
La definizione stessa del teorema di Pitagora recita: In un triangolo rettangolo, il quadrato che si può formare sull’ipotenusa (un quadrato con il lato uguale all’ipotenusa) ha l’area uguale alla somma delle aree dei quadrati che si può formare allo stesso modo sulle sue gambe (i due lati più corti di un triangolo rettangolo). Questa regola è stata scoperta da Pitagora!
Ricordiamo brevemente come vengono chiamati i diversi lati di un triangolo rettangolo. Il lato più lungo è sempre contrassegnato con la lettera c (lettera latina minuscola c) e si chiama ipotenusa. I due lati di un triangolo rettangolo che sono più corti dell’ipotenusa sono chiamati cateti e sono indicati con a e b (lettere latine minuscole a e b). In un triangolo rettangolo, l’angolo formato dai cateti (lati a e b) è sempre dritto, cioè è esattamente 90 gradi. Gli altri due angoli (angoli situati sull’ipotenusa) sono sempre acuti, cioè la loro dimensione è inferiore a 90 gradi. Clicca qui per vedere quali tipi di angoli esistono!
Formula del teorema di Pitagora
Una delle formule più utilizzate in geometria e matematica, la formula che descrive il teorema di Pitagora è:
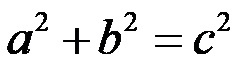
La composizione della formula del teorema di Pitagora ci permette di usarlo per calcolare la lunghezza di un lato sconosciuto di un triangolo rettangolo, se gli altri due lati sono noti. Ad esempio, se si conosce la lunghezza dei cateti, è possibile calcolare facilmente la lunghezza dell’ipotenusa, oppure se si conoscono la lunghezza dell’ipotenusa e di uno dei cateti, è possibile determinare facilmente la lunghezza dell’altro cateto.
Di seguito, nei pochi esempi, puoi vedere come viene applicato il teorema di Pitagora per determinare la lunghezza di un lato sconosciuto in un triangolo rettangolo! Ti consigliamo di dare un’occhiata agli esempi qui sotto!
Esempi
Esempio 1. Calcola la lunghezza dell’ipotenusa di un triangolo rettangolo, sapendo che le lunghezze dei suoi cateti sono 8 cm e 15 cm!
In questa situazione, nota la lunghezza delle due gambe, possiamo immediatamente sostituire la loro lunghezza nella formula del teorema di Pitagora. Questa sostituzione di valori produce l’espressione data nell’immagine qui sotto!

Nel passaggio successivo, ridimensioniamo entrambi i valori, quindi otteniamo:
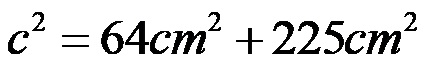
Calcoliamo la somma dei valori appena ottenuti:
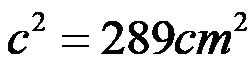
Infine, per calcolare la lunghezza dell’ipotenusa, calcoliamo la radice del valore numerico che si trova a destra dell’equazione.
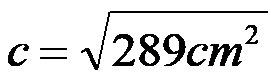
La lunghezza dell’ipotenusa del triangolo rettangolo dell’esempio 1 è 17 centimetri!
Logicamente, le possibilità offerte dal teorema di Pitagora si riferiscono anche al calcolo della lunghezza di un cateto sconosciuto se si conoscono l’altro cateto e l’ipotenusa. In tale situazione, in relazione a come viene contrassegnata la gamba sconosciuta in un caso specifico, è possibile utilizzare una delle seguenti formule per risolvere:

Se la gamba etichettata a è sconosciuta, usi la formula a sinistra, ma se la gamba etichettata b è sconosciuta, usi la formula a destra!
Risolviamo un esempio del genere! Dai un’occhiata all’esempio 2 qui sotto!
Esempio 2. Un triangolo rettangolo ha l’ipotenusa lunga 29 decimetri. Calcola la lunghezza di una delle sue zampe, se l’altra gamba è lunga 21 decimetri!
Se indichiamo la lunghezza della gamba sconosciuta con a, allora possiamo utilizzare direttamente la formula trasformata dal lato sinistro in alto, colorata in rosso. Sostituendo i valori indicati per l’ipotenusa e la gamba nota, si ottiene l’espressione:
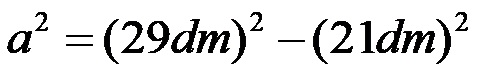
Valutiamo:
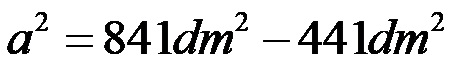
Calcoliamo la differenza dei numeri:
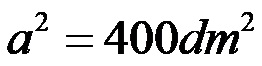
Finalmente tifiamo!
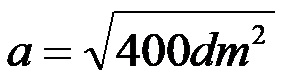
La lunghezza della gamba sconosciuta del secondo esempio è di 20 decimetri!
Applicazione del teorema di Pitagora
Ti consigliamo di guardare il contenuto del video qui sotto! In esso puoi vedere come viene definito il teorema, diversi esempi di calcolo della lunghezza di un lato sconosciuto e diverse combinazioni di terne pitagoriche (numeri interi che potrebbero essere le lunghezze dei lati di un triangolo rettangolo).
Il teorema di Pitagora è ampiamente utilizzato in geometria e matematica in generale. La presenza di un triangolo rettangolo in corpi geometrici regolari, spazio, forme immaginarie, corpi e spazio, consente a questo teorema di essere utilizzato in molte situazioni diverse e aiuta a risolvere molti problemi matematici. Molti dei successi ottenuti nel campo della trigonometria sono stati realizzati grazie a questo teorema.
Tags: Di Pitagora, Esempi, Formula, Pitagora, Problema, Teorema
 Attendere prego...
Attendere prego...