Questo post riguarda il teorema del seno, uno dei teoremi più importanti della trigonometria. Questo teorema rende possibile utilizzare la sua applicazione per calcolare la lunghezza di un lato di qualsiasi triangolo o la dimensione degli angoli dei triangoli. Ecco perché nel post di oggi spiegheremo bene cos’è e come si applica in esempi e problemi matematici specifici. La pagina stessa ha una guida video in fondo che mostra molto chiaramente come viene definito per i diversi triangoli.
Come viene definito il teorema del seno
Per trarre la conclusione che chiamiamo teorema del seno, un triangolo dovrebbe essere diviso in due triangoli rettangoli abbassando una delle tre altezze. La lunghezza dell’altezza è un lato comune per entrambi i diversi triangoli rettangoli. La sua lunghezza è espressa attraverso i membri del primo e del secondo triangolo, quindi poiché entrambe le espressioni hanno un risultato identico, possiamo equipararle tra loro. Ecco come viene definito il teorema del seno. Guarda l’immagine qui sotto e nota come un triangolo è diviso in due triangoli rettangoli abbassando una delle altezze!
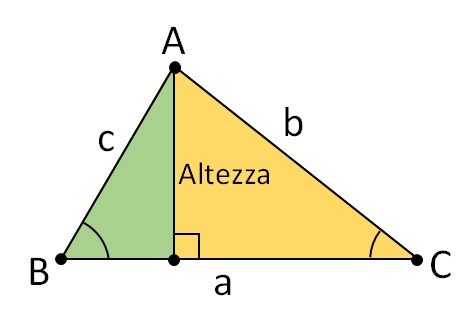
Per il triangolo verde dell’immagine sopra, possiamo scrivere le seguenti formule:
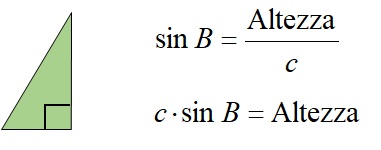
Allo stesso modo, per il triangolo arancione si possono ricavare le seguenti formule:
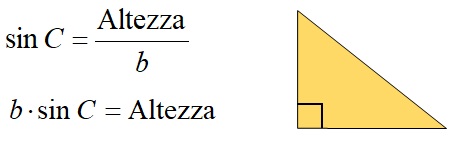
Logicamente, poiché entrambe le formule (del triangolo verde e di quello arancione) sono uguali alla lunghezza dell’altezza, possiamo scrivere che tra loro esiste un’uguaglianza. Si applica la formula:
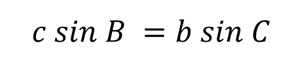
Da dove possiamo facilmente derivare la conclusione per la prima parte del teorema del seno:

Se ripetiamo questa procedura abbassando tutte e tre le altezze allo stesso modo, otteniamo l’intero contenuto del teorema del seno che recita:
Applicazione
L’applicazione del teorema del seno è enorme! Questo teorema è uno dei teoremi più utilizzati in trigonometria, geometria e matematica in generale. L’applicazione principale del teorema del seno si riferisce alla determinazione della lunghezza di un lato di lunghezza sconosciuta, o della dimensione di un angolo in un triangolo di cui non conosciamo la dimensione.
Di seguito hai l’opportunità di considerare un esempio di calcolo della lunghezza di un lato di un triangolo e della dimensione di un angolo utilizzando.
Esempio 1. Calcola quanto è lungo il lato x del triangolo nella figura qui sotto!
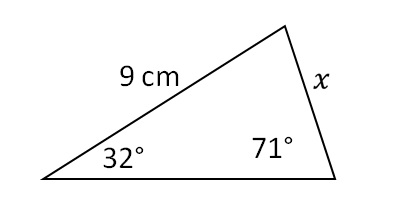
Dai dati forniti nella figura sopra si può facilmente capire che abbiamo dati sufficienti per applicare il teorema del seno. La relazione che dobbiamo stabilire è:
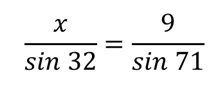
Da cui segue che:
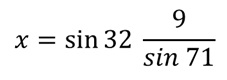
Calcolando i valori delle funzioni trigonometriche si ottiene il risultato finale che si riferisce alla lunghezza del lato incognito del triangolo:
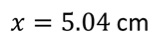
Esempio 2. Calcola la dimensione dell’angolo x nel triangolo nell’immagine qui sotto!
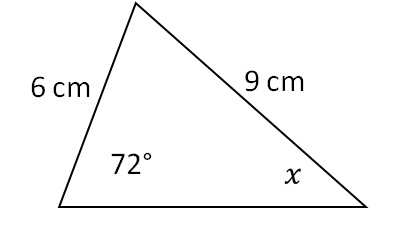
Applicando il teorema del seno, scriviamo la relazione:
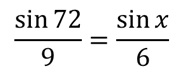
Da cui segue che:
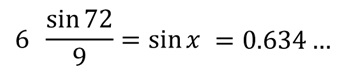
Per determinare finalmente facilmente che la dimensione dell’angolo sconosciuto è:
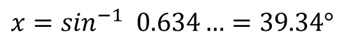
Prove video ed esempi
Il materiale video a tua disposizione con un solo clic qui sotto contiene una dimostrazione di come viene definito per diversi triangoli. Inoltre nel video puoi vedere un numero enorme di esempi risolti in cui la lunghezza dei lati di diversi triangoli o la dimensione dei loro angoli sono determinati utilizzando il teorema del seno! Ti consigliamo di rivedere il maggior numero di esempi possibile!
Tags: Applicazione, Definito, Del, Esempi, Esempio, Problema, Seno, Teorema

 Attendere prego...
Attendere prego...