La somma degli angoli esterni di un poligono è 360 gradi! Dimostrerò questa affermazione nel video, disponibile di seguito, con due diversi tipi di dimostrazioni geometriche. Oltre a ciò, non ti mostreremo come funziona questa regola e il fatto che puoi usarla in un compito matematico specifico in cui devi calcolare le dimensioni di un angolo interno o esterno di un dato poligono. Puoi vedere più attività ed esempi di questo tipo nello stesso video, che include anche una dimostrazione della somma degli angoli esterni in un poligono.
Dimostrazione della somma degli angoli esterni in un poligono
Oggi esistono diverse prove del fatto che la somma degli angoli esterni di un poligono è esattamente 360 gradi. Tuttavia, la rappresentazione geometrica è sempre una buona variante per consentire ad ogni lettore di convincersi facilmente della dimostrazione stessa. Ecco perché confermeremo con una dimostrazione geometrica che la somma degli angoli esterni di un poligono è 360 gradi.
Dai un’occhiata alle immagini qui sotto in dettaglio!
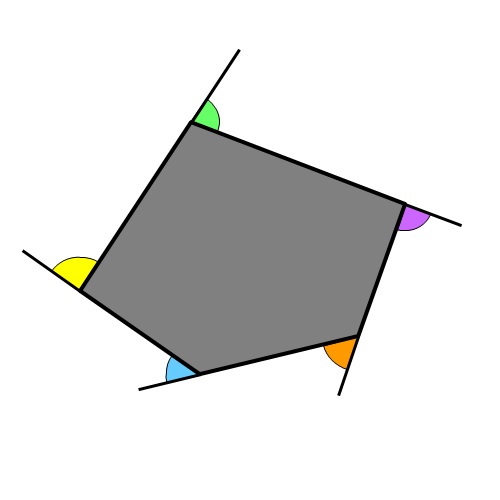
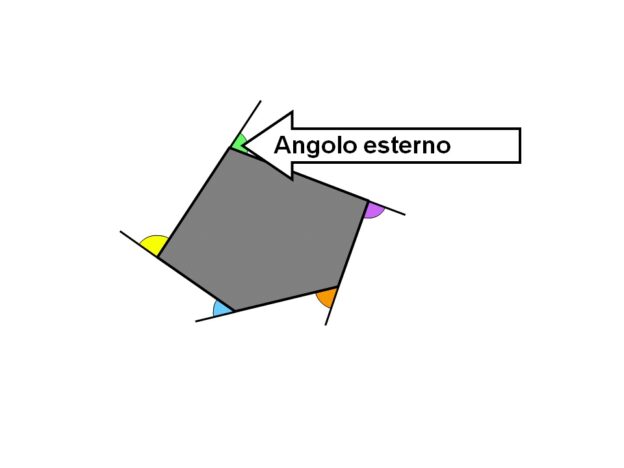
Nella prima immagine, tutti gli angoli esterni di un dato poligono sono contrassegnati in colori diversi.
Nella prossima immagine, con la combinazione appropriata, è molto chiaro che quando li incolliamo insieme, formano un intero cerchio, cioè esattamente 360 gradi. La dimostrazione è semplice ma presenta molto chiaramente la realtà che la somma degli angoli esterni in un poligono è in realtà 360 gradi.
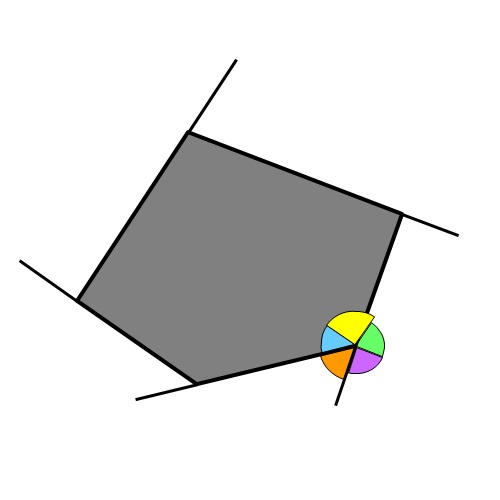
Senza questa dimostrazione per generalizzarlo ad altri poligoni, confermeremo che ciò è valido per qualsiasi poligono indipendentemente dal numero dei suoi angoli.
Vedrai come calcolare la somma degli angoli interni di un poligono!
Problemi con la somma degli angoli esterni in un poligono
In ogni caso, il significato della somma degli angoli esterni in un poligono è applicabile in compiti specifici in cui questa regola può aiutarci anche a determinare le dimensioni di un angolo esterno sconosciuto (se conosciamo le dimensioni di tutti gli altri angoli esterni), quindi in alcune situazioni anche ad un angolo interno di dimensione sconosciuta. Nel seguito, esamineremo due esempi così diversi!
Esempio 1. Calcola le dimensioni dell’angolo esterno del poligono nella parte inferiore dell’immagine di cui non si conosce la dimensione!
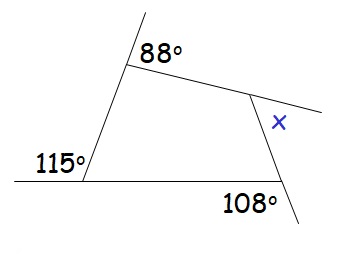
Ovviamente un poligono è un quadrilatero che ha quattro angoli interni e quattro esterni. Tre dei suoi quattro angoli esterni misurano 115, 108 e 88 gradi. Il quarto angolo, di cui non si sa quanto sia grande, può essere calcolato grazie alla regola della somma degli angoli esterni di un poligono. Pertanto, calcolando dalla somma totale di 360, sottrarremo la somma dei tre angoli esterni di cui conosciamo la dimensione.
Calcolerò le dimensioni dell’angolo sconosciuto con l’espressione “metà”:
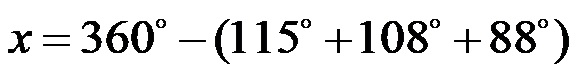
Per prima cosa calcoliamo la somma dei numeri tra parentesi.
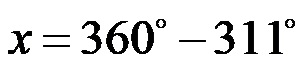
Alla fine, sottraiamo i numeri per ottenere il valore finale dell’angolo sconosciuto.
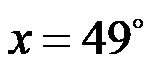
X ha 49 gradi!
Esempio 2. Calcola le dimensioni dell’angolo esterno del poligono nella parte inferiore dell’immagine di cui non conosciamo le dimensioni!
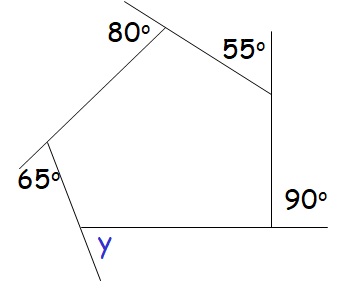
L’immagine sopra mostra un pentagono con cinque angoli esterni. Quattro di loro hanno 90, 80, 65 e 55 gradi. Il quinto angolo y non si sa quanto sia grande. Logicamente, proprio come nell’esempio precedente, calcolerò la sua dimensione come differenza tra 360 e la somma degli altri quattro angoli.
Le dimensioni di agolot y possono essere calcolate utilizzando l’espressione:
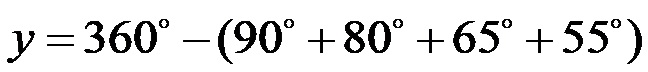
Anche in questo caso, prima calcoliamo la somma dei numeri tra parentesi.
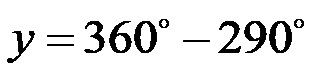
Alla fine, calcoliamo la differenza in numeri!
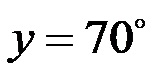
Y è di 70 gradi!
Esempi video e attività
Il materiale video qui sotto contiene molte dimostrazioni, esempi e problemi matematici in cui viene utilizzato il fattore secondo cui la somma è di 360 gradi. Il video contiene molti metodi di presentazione interessanti, quindi ti consigliamo di guardarne l’intero contenuto. Vi auguriamo il meglio!
Tags: 360, Angoli, Degli, Esempi, Esterni, Gradi, Poligono, Problema, Somma
 Attendere prego...
Attendere prego...