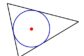
La simmetria assiale è un tipo di trasformazione geometrica in cui la simmetria è determinata o avviata su due lati diversi rispetto a un asse ottico principale (linea).
Asse di simmetria
Inoltre, se due punti (normalmente con un angolo di 90 gradi) si trovano su due lati diversi dell’asse di simmetria, alla stessa distanza e sullo stesso piano, allora quei due punti sono considerati simmetrici rispetto a quell’asse di simmetria!
Allo stesso modo, se tutti i punti di una figura geometrica sono equidistanti su due lati diversi sullo stesso piano di un’altra figura geometrica, allora si può dire che quelle due figure geometriche sono simmetriche rispetto a quell’asse di simmetria.
Un asse di simmetria può essere determinato anche per una figura, se quella figura geometrica può essere divisa in due parti identiche che soddisfano le condizioni di simmetria di cui sopra rispetto ad un dato asse di simmetria! Molto spesso, gli studenti pensano se una figura geometrica possa essere piegata a metà, quindi, se possibile, il punto di piegatura è esattamente l’asse di simmetria stesso!
Figure assialsimmetriche
Alcune delle figure geometriche più famose appartengono alla classe delle figure assialsimmetriche! Una figura geometrica è assialsimmetrica se ha almeno un asse di simmetria! Naturalmente esistono anche figure geometriche che hanno più di un asse di simmetria!
Diamo un’occhiata ad alcune figure geometriche caratteristiche che sono assialsimmetriche!
Le figure geometriche assialsimmetriche includono:
Un triangolo equilatero ha tre assi di simmetria!
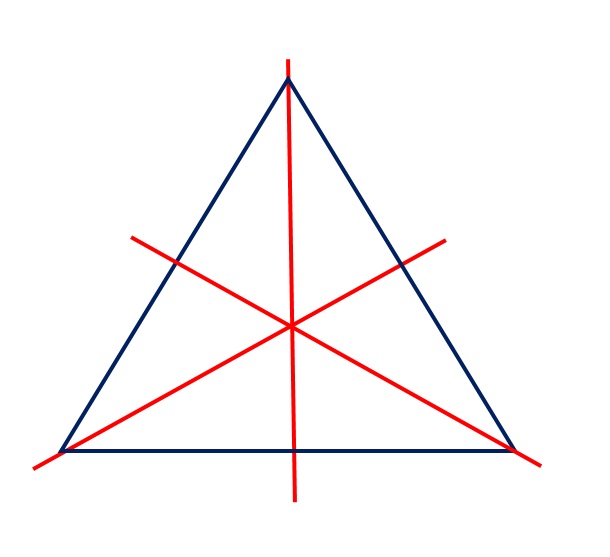
Un triangolo isoscele ha un unico asse di simmetria!
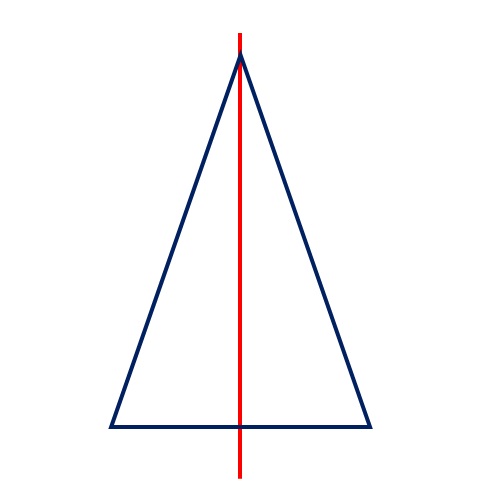
Sai come calcolare l’area di un triangolo isoscele?
Un rettangolo ha due assi di simmetria!
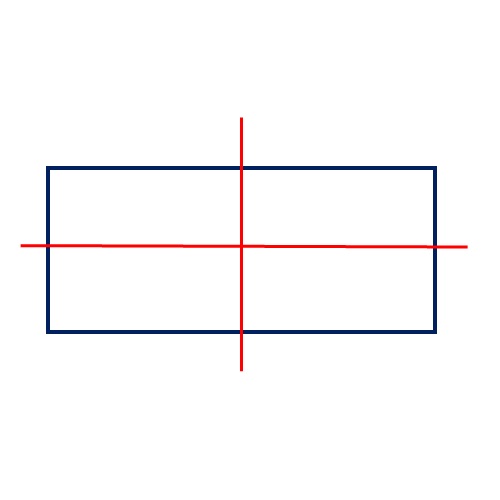
Un quadrato ha quattro assi di simmetria!
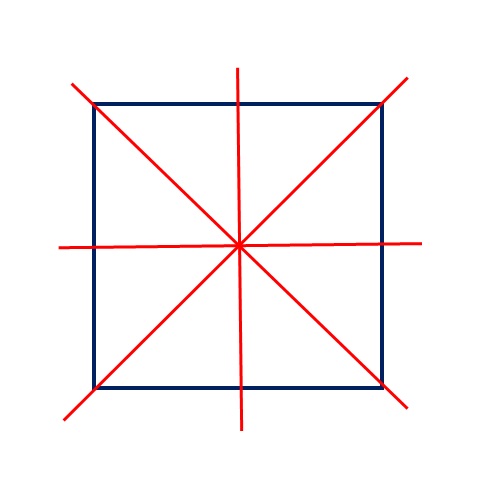
Un trapezio isoscele ha un asse di simmetria!
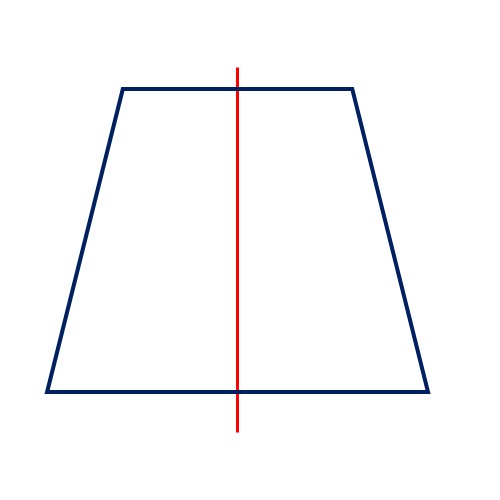
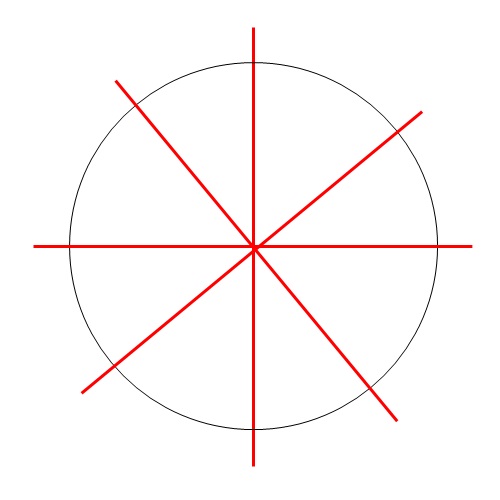
Un cerchio ha infiniti assi di simmetria!
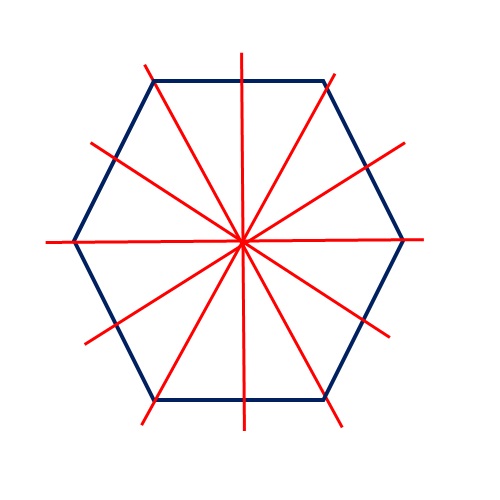
Alcune figure geometriche che hanno più di quattro lati o angoli possono avere un asse di simmetria, ma molto spesso si tratta dei cosiddetti poligoni regolari, i cui lati e angoli sono uguali tra loro! Esempio Un esagono regolare ha sei assi di simmetria!
Guarda come costruire una bisettrice dell’angolo!
Simmetria assiale in un sistema di coordinate
Come tipo di trasformazione geometrica, spesso abbiamo bisogno di utilizzare la simmetria degli assi in un sistema di coordinate con un asse di simmetria strettamente definito dato in relazione all’asse delle coordinate x,y o qualsiasi altra linea che di nuovo abbia dato determinati valori in relazione a l’asse x o l’asse y.
Il fatto stesso che due figure geometriche siano simmetriche rispetto a un asse di simmetria, i loro punti corrispondenti dovrebbero essere equidistanti dall’asse, parla del fatto che quando è necessario determinare geometricamente una figura simmetrica, è sufficiente ottenere ciascuna dei suoi punti ad uguale distanza dall’asse sul lato opposto ad esso!
Osserva attentamente le immagini qui sotto per capire esattamente cosa bisogna fare!
Esempio 1. Costruisci un’immagine della figura geometrica B con simmetria assiale rispetto all’asse di simmetria y= -2!
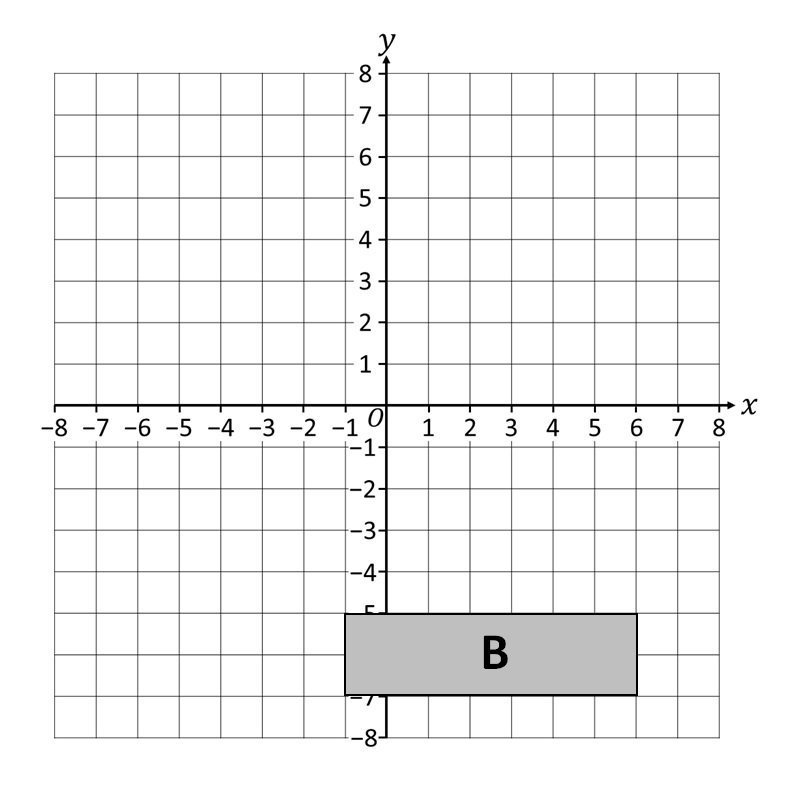
Per prima cosa disegniamo l’asse di simmetria y=-2!
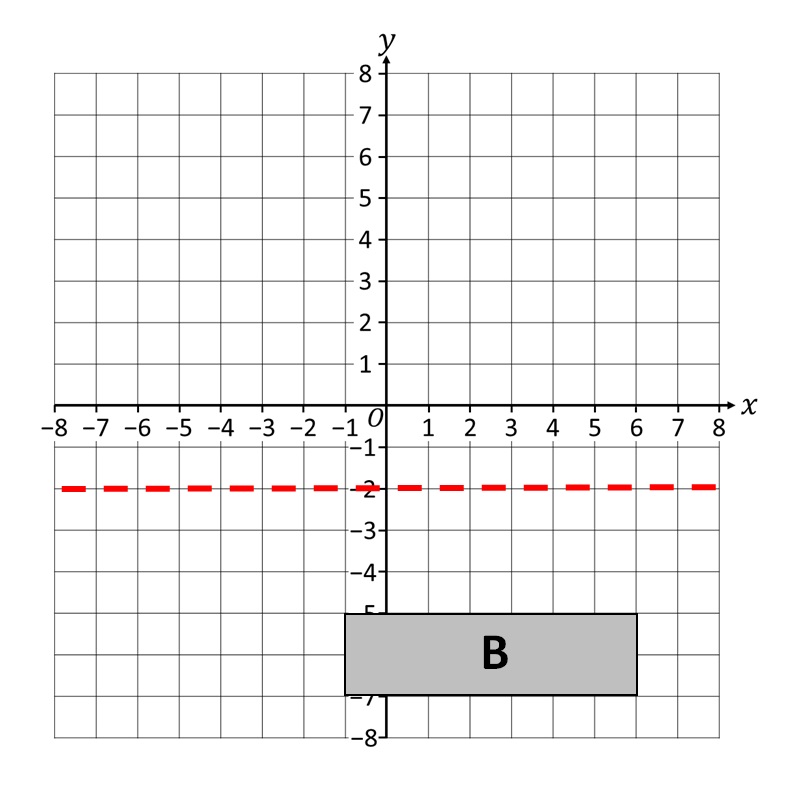
Quindi per ciascun vertice della figura geometrica B determiniamo la sua immagine corrispondente ad uguale distanza dal lato opposto dell’asse di simmetria. Inizieremo con il primo vertice!
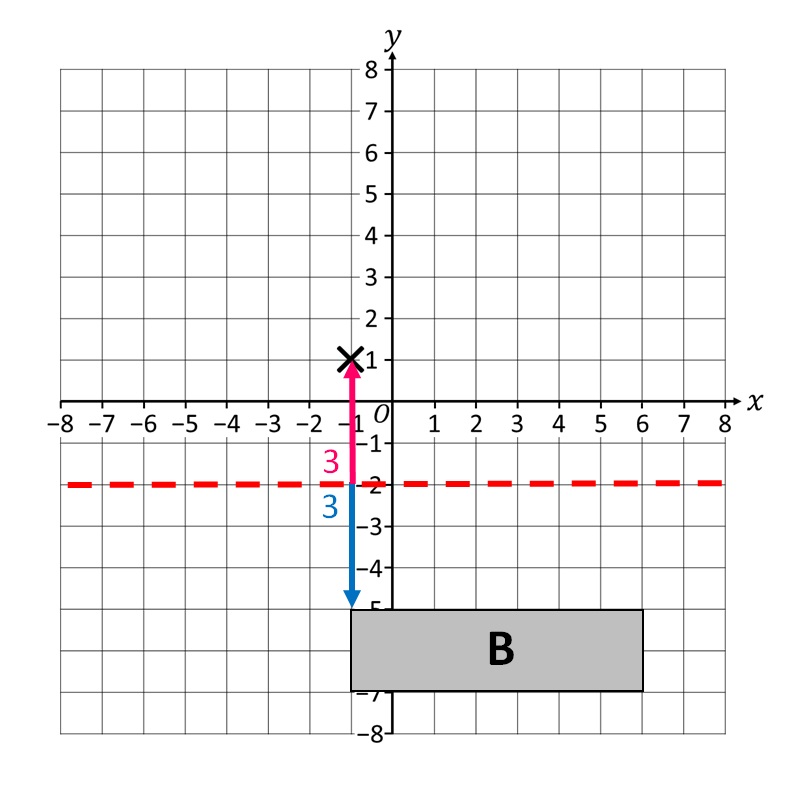
Il secondo vertice sta arrivando!
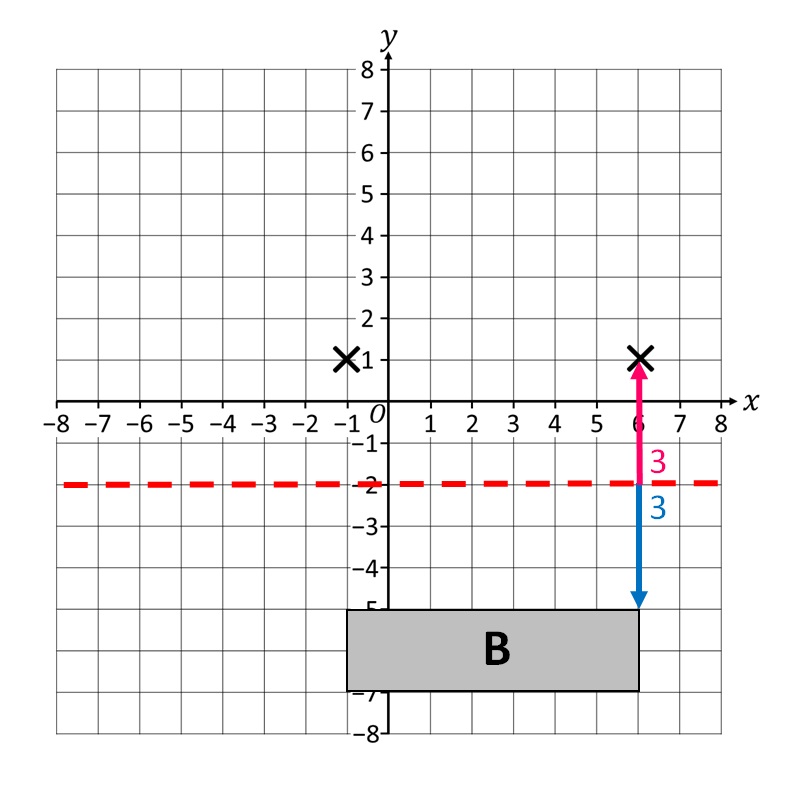
Poi mappiamo anche il terzo vertice!
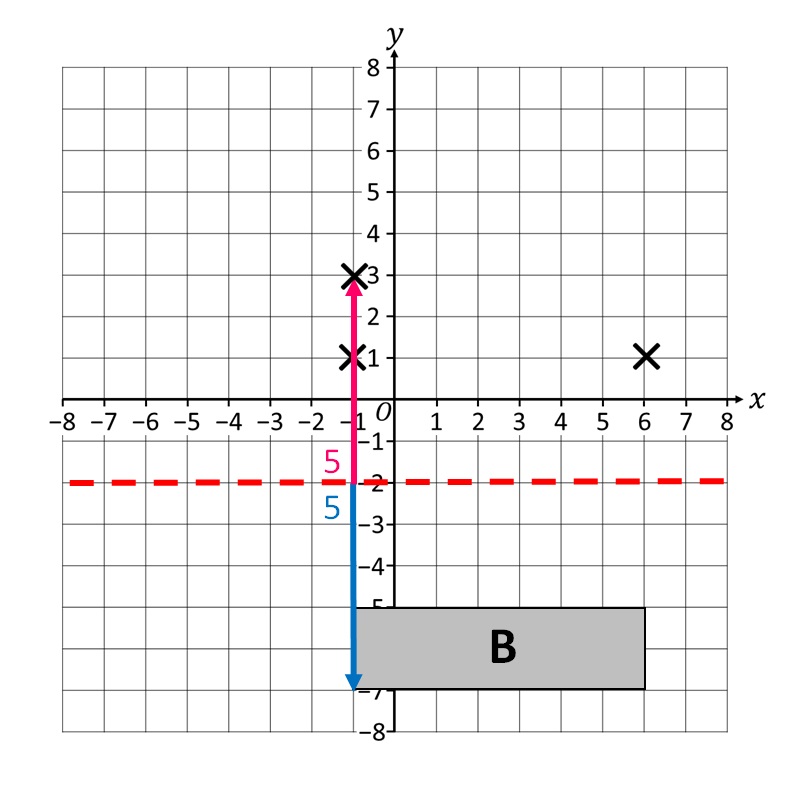
Infine terminiamo con la mappatura dell’ultimo vertice!
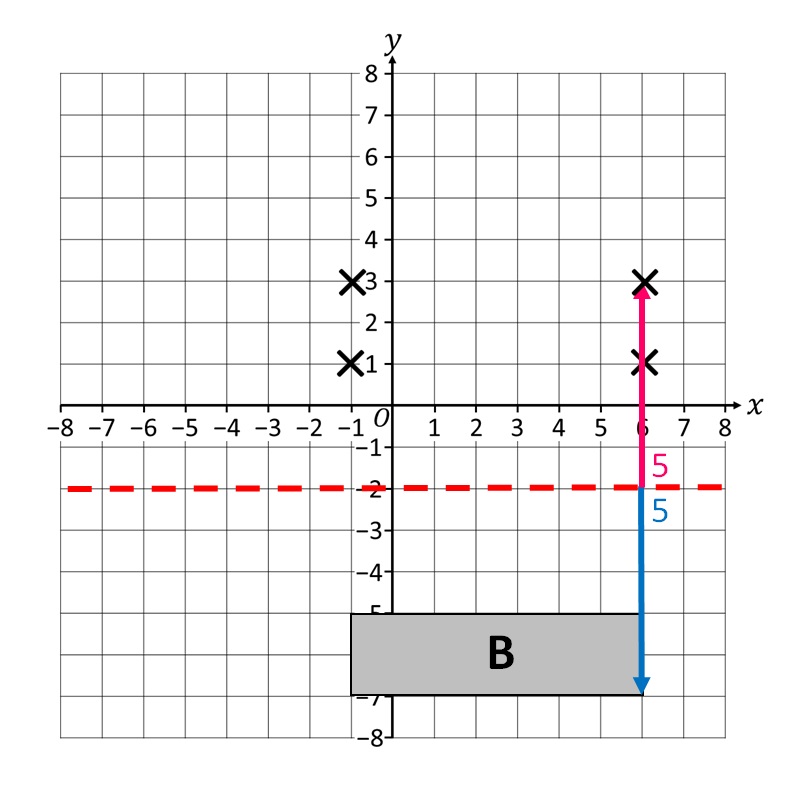
Il passo finale è disegnare l’intera immagine, corrispondente e simmetrica alla figura geometrica B! Il risultato finale dovrebbe assomigliare all’immagine qui sotto!
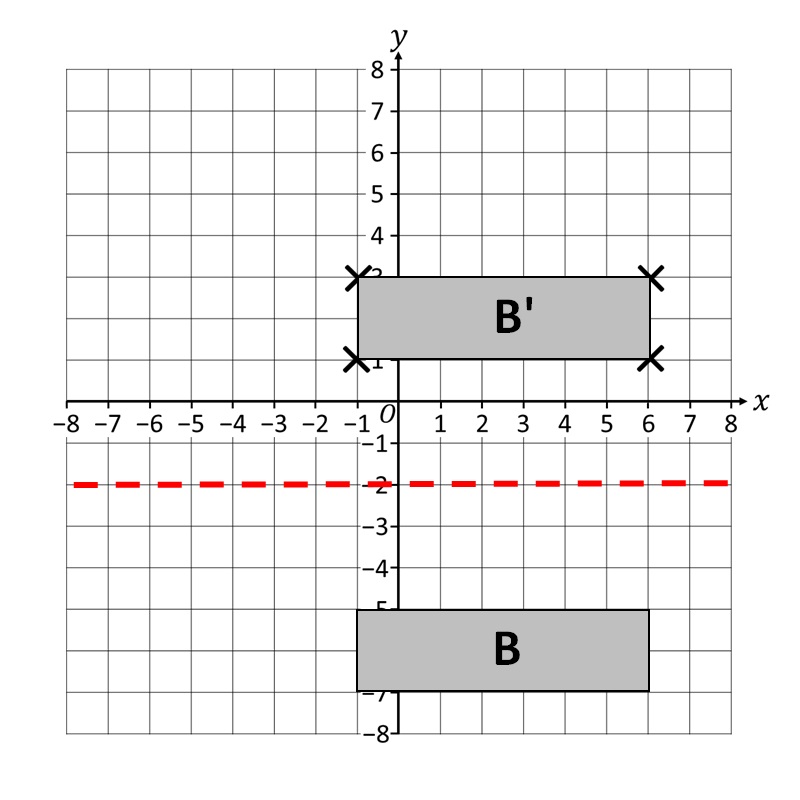
Non è affatto difficile, vero? Devi solo cercare di essere preciso affinché l’immagine sia il più chiara e precisa possibile, e quindi più bella!
Esempi video per simmetria assiale
Il materiale video, a cui puoi accedere facendo clic sull’icona video qui sotto, ti dà accesso ad esempi presentati in modo estremamente chiaro di mappatura assialsimmetrica in un sistema di coordinate. Ti consigliamo di dare un’occhiata a questi esempi per capire la differenza rispetto ad assi di simmetria posizionati e definiti diversamente!
Tags: Asse, Assiale, Assialsimmetriche, Figure, Simmetria
 Attendere prego...
Attendere prego...