Quali competenze devi avere per calcolare con successo il perimetro e area di figure composte? Qui in questo testo descriveremo tutto quello che devi sapere per poter calcolare il perimetro e l’area di figure geometriche 2D complesse. Allo stesso tempo, procederemo passo dopo passo nelle spiegazioni in modo che ogni lettore possa capire il punto in cui risolve questi problemi matematici.
Conoscenze e competenze richieste per perimetro e area di figure composte
Chiunque cerchi di risolvere il problema del calcolo del perimetro e area di figure composte dovrebbe conoscere le singole formule per calcolare il perimetro e l’area di figure 2D caratteristiche come un quadrato, un rettangolo, un rombo, ecc.
A volte, in alcuni compiti individuali, è molto importante usare il pensiero logico per trarre conclusioni corrette sulla lunghezza di alcuni lati di una figura geometrica complessa che all’inizio non è affatto nota. Tuttavia, in quelle situazioni, ha fornito sufficienti informazioni iniziali su quel lato, o su quella parte di quel lato, per poterlo determinare senza alcun problema. La nostra raccomandazione è di fare attenzione in quelle specifiche situazioni perché è molto facile commettere un errore!
Consideriamo una di queste situazioni in cui dobbiamo determinare la lunghezza di un lato di una figura geometrica complessa che non conosciamo! Guarda l’esempio qui sotto!
Esempio 1. Qual è la lunghezza del lato sconosciuto della figura geometrica complessa indicata nella figura seguente?
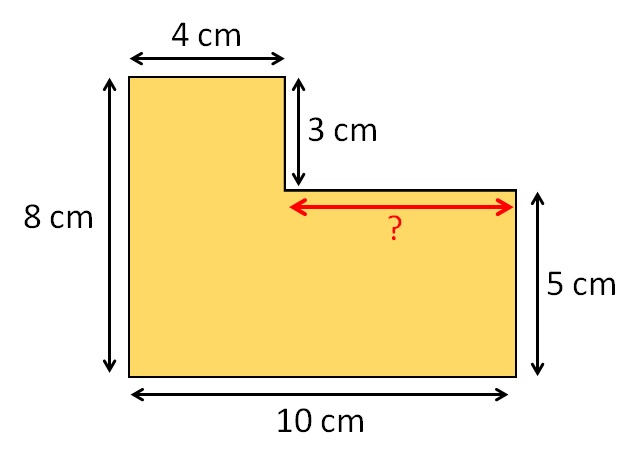
Il lato sconosciuto è segnato in rosso! Ovviamente, la lunghezza di quel lato sconosciuto può essere determinata come la differenza tra i lati paralleli rispetto al lato sconosciuto. Logicamente sottraiamo il lato più corto dal lato più lungo, ovvero:
10 cm – 4 cm = 6 cm
La lunghezza del lato sconosciuto è di 6 centimetri!
Perimetro di una figura geometrica complessa
Se possiedi tutte le conoscenze e le competenze necessarie elencate sopra, puoi avvicinarti alla determinazione del perimetro di una figura geometrica complessa. Per determinare il perimetro occorre calcolare la somma di tutti i lati della figura complessa. Nel secondo esempio ti aiuteremo a calcolare il perimetro della figura complessa per la quale abbiamo già determinato la lunghezza del lato sconosciuto nell’esempio numero uno. Vediamo che aspetto ha!
Esempio 2. Calcola il perimetro della figura complessa mostrata nell’immagine qui sotto!
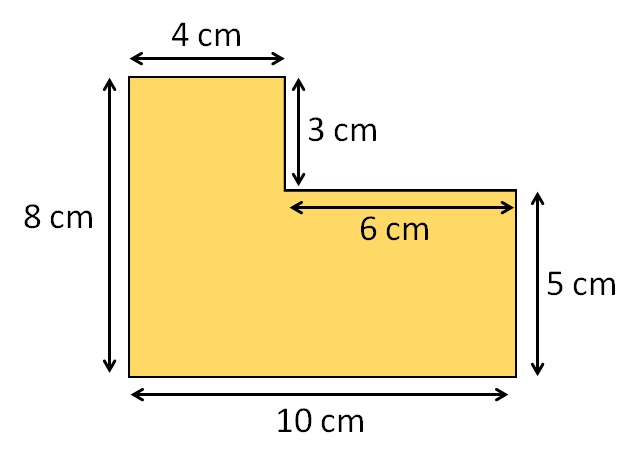
Scegliamo semplicemente un punto di partenza da cui vogliamo iniziare e calcoliamo la somma delle lunghezze di tutti i lati della figura geometrica complessa. Nel fare ciò, fai attenzione a non tralasciare nessuno dei lati perché ciò porterebbe ad una soluzione errata!
Il calcolo dovrebbe assomigliare a questo:
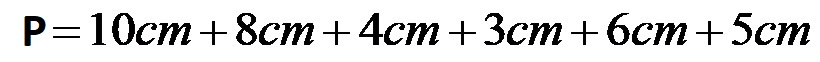
Il perimetro della figura complessa è di 36 centimetri!
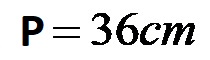
Area di una figura complessa
La procedura per calcolare l’area di una figura complessa è una procedura matematica più complicata rispetto al calcolo del suo perimetro. Per calcolare l’area, dobbiamo immaginare la figura complessa come una combinazione di forme geometriche 2D regolari. Se rappresentiamo la sua intera superficie come una combinazione delle superfici di un quadrato, di un rettangolo o di qualche altra forma 2D regolare, allora la somma delle loro superfici è in realtà la superficie della forma geometrica complessa.
A volte possiamo anche immaginare parti esterne della figura complessa che insieme ad essa costruiscono una forma geometrica regolare. In tal caso, il compito può essere calcolato come differenza tra il tutto (figura complessa + parte esterna) e la parte esterna.
Come si può facilmente comprendere, l’area di una figura complessa può essere calcolata in diversi modi. Presenteremo di seguito come calcolare l’area della stessa figura complessa in due modi diversi!
Area di una figura complessa come insieme di figure interne
Torniamo alla nostra figura complessa di cui abbiamo già determinato il lato e il perimetro sconosciuti! Considera attentamente la soluzione del seguente esempio!
Esempio 3. Calcola l’area della figura complessa di cui abbiamo già determinato il perimetro nell’esempio precedente!
Il nostro primo obiettivo in questa situazione è rappresentare questa figura complessa come una combinazione di più figure regolari! Una di queste opportunità è presentata nell’immagine qui sotto!
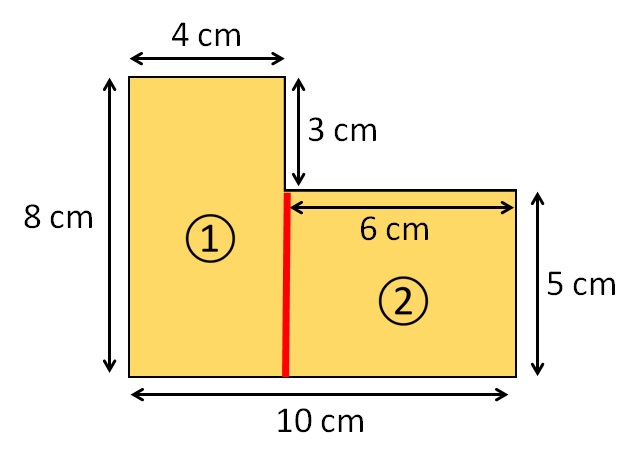
I numeri 1 e 2 indicano due diversi rettangoli che insieme ricoprono l’intera superficie della figura complessa. Pertanto l’area dei due rettangoli insieme ha la stessa area della figura complessa. Pertanto, possiamo calcolare l’area di una figura complessa utilizzando la formula per l’area di un rettangolo, come segue:
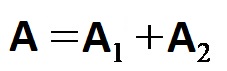
Stiamo inserendo la formula per determinare il area di un rettangolo!
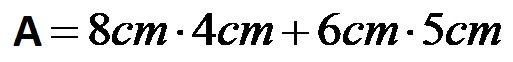
Calcoliamo i singoli prodotti.
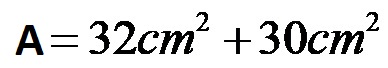
Infine aggiungiamo i due valori!
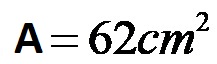
L’area della figura complessa con il primo metodo è di 62 centimetri quadrati!
Area di una figura complessa distinta dalle parti immaginarie
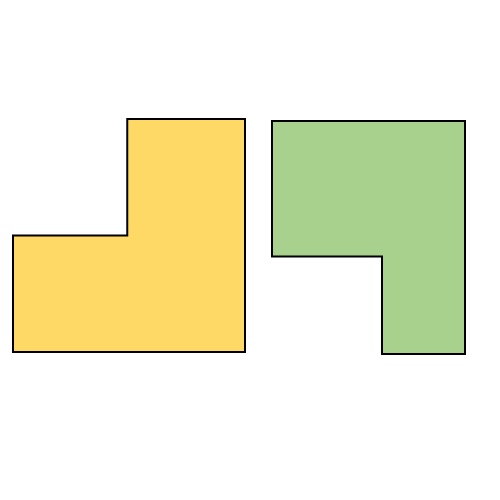
Presenteremo la stessa figura geometrica complessa del terzo esempio come una figura geometrica regolare intera immaginata! Una di queste possibilità è data nell’immagine qui sotto:
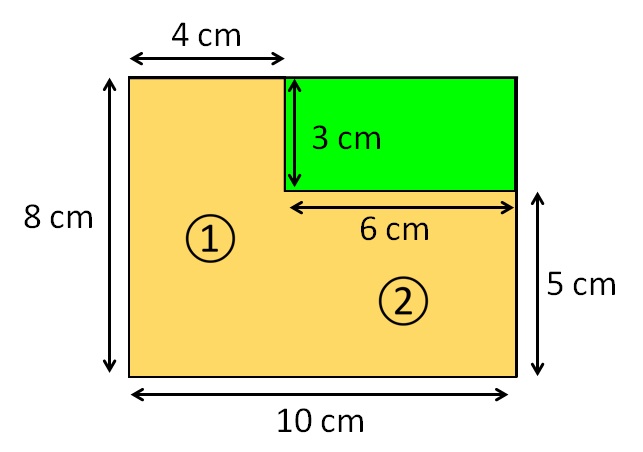
Dall’immagine sopra si vede chiaramente che prima sulla figura complessa ed ediamo una parte aggiuntiva (la parte colorata di verde) con la quale quella figura insieme costruisce un rettangolo. È molto facile vedere che se guardiamo le cose in questo modo, allora l’area di una figura complessa può essere calcolata come la differenza tra l’area dell’intera figura (complessa + verde) e l’area addizionale (l’area parte verde). Qui con A con indice c indichiamo l’area dell’intera figura, e con A con indice z la parte verde. Il calcolo è riportato di seguito!
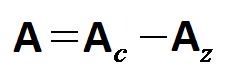
Per prima cosa inseriamo la formula per l’area di un rettangolo (entrambe le forme sono rettangolari).
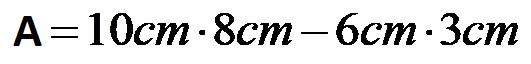
Adesso calcoliamo i singoli prodotti!
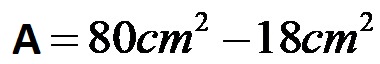
Infine, sottraiamo i due valori!
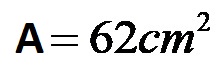
L’area della figura complessa con il secondo metodo è di 62 centimetri quadrati!
Un’altra prova che lo stesso problema matematico può essere risolto in molti modi diversi. Questo esempio conferma che quando si determina l’area di una figura complessa, qualunque sia il modo in cui si pensa, purché lo si faccia nel modo giusto, si può arrivare alla soluzione corretta.
Esempi video per perimetro e area di figure composte
Il materiale video seguente contiene molti esempi interessanti di calcolo del perimetro e dell’area di una figura complessa. Guarda quanti più esempi possibili per considerare diverse situazioni problematiche che ti aiuteranno in futuro a risolvere facilmente compiti in cui devi calcolare il perimetro e l’area di figure complesse!
Tags: Area, Composte, Esempi, Figure, Formula, Perimetro, Perimetro e area
 Attendere prego...
Attendere prego...