Sei pronto per imparare tutto sulla moltiplicazione tra frazioni! Qui in questa pagina ti faremo imparare come moltiplicare una frazione per una frazione, ma nella seconda parte di questo sito potrai vedere come moltiplicare una frazione per un numero intero! Vale la pena ricordare innanzitutto che questa operazione matematica è molto più semplice dell’addizione o della sottrazione di frazioni. Di seguito, entrambi i tipi di moltiplicazione delle espressioni che coinvolgono le frazioni vengono spiegati passo dopo passo per aiutarti a imparare tutto su questa attività matematica.
Per entrambi i diversi tipi di moltiplicazione tra frazioni, sono disponibili materiali in forma scritta e video. Ti consigliamo vivamente di guardare tutti gli esempi video che abbiamo preparato per te, perché attraverso la ripetizione di diversi esempi è più facile imparare e memorizzare il materiale didattico più velocemente.
Come moltiplicare tra frazioni
Per moltiplicare con successo una frazione per una frazione segui i passaggi seguenti che sono molto semplici!
- Per ottenere il numeratore della soluzione, calcolare il prodotto dei singoli numeratori
- Per ottenere il denominatore della soluzione, calcolare il prodotto dei singoli denominatori
Le regole di cui sopra si applicano quando si moltiplicano tra due frazioni, ma puoi usare la stessa regola senza alcun problema quando si moltiplicano tre o più frazioni! Vedi l’esempio risolto qui sotto!
Esempio 1: Calcola il prodotto delle due frazioni:
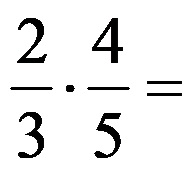
Esercitiamo i passaggi precedenti della regola per moltiplicare le frazioni. Dovrebbe sembrare come questo:
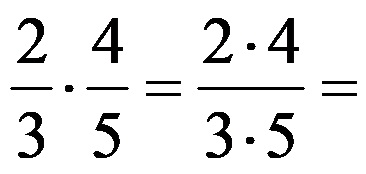
Calcoliamo ancora i singoli prodotti al numeratore e al denominatore! La soluzione finale assume la forma seguente:
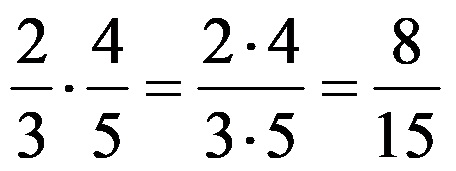
Nel video qui sotto puoi vedere molti esempi che hanno una soluzione completa. Ti consigliamo, dopo aver esaminato alcuni esempi, di interrompere il video in determinati segmenti per verificare se puoi prevedere correttamente il risultato.
Consideriamo ora cosa succede in quella situazione in cui è necessario fare la moltiplicazione tra frazioni e numeri interi! In questa parte della pagina hai l’opportunità di vedere molti esempi che coprono diversi tipi di frazioni che devono essere moltiplicate per un numero intero!
Moltiplicare una frazione per un numero intero è un problema semplice che probabilmente richiederà solo pochi minuti. Trascorri qualche minuto qui, esamina tutti gli esempi e padroneggerai con successo la tecnica stessa della moltiplicazione delle frazioni.
Come moltiplicare una frazione per un numero intero
La regola per moltiplicare le frazioni per numeri interi è molto semplice. Semplicemente per completare il calcolo dobbiamo moltiplicare il numero intero e il numeratore della frazione, mentre il denominatore rimane lo stesso! Vediamo come appare negli esempi risolti qui sotto!
Esempio 2: Calcola il prodotto!
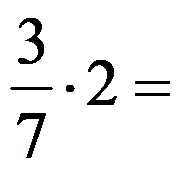
Il calcolo in questo caso si riduce al calcolo del prodotto del numero intero 2 e del numeratore 3. Il loro prodotto è il numeratore della frazione che è la soluzione del problema. D’altra parte, il denominatore della frazione – il numero 7 rimane lo stesso nel risultato. Puoi vedere l’intero calcolo qui sotto!
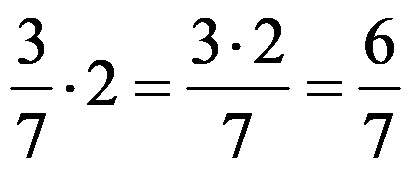
È molto importante, oltre all’operazione stessa di moltiplicazione delle frazioni, prestare attenzione al tipo di frazione nel risultato. Se necessario, tale frazione dovrebbe essere semplificata o convertita in un numero misto.
Esempio 3: Calcola il prodotto tra una frazione e un numero intero:
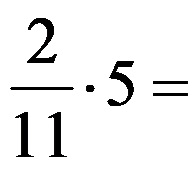
Applichiamo nuovamente la stessa regola e ripetiamo il procedimento che abbiamo già applicato nell’esempio precedente!
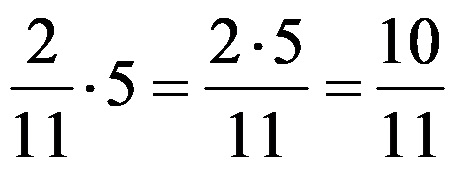
In tutti e tre gli esempi risolti sopra, si ottiene un risultato che è esso stesso in forma regolare.
In tutorial separati tratteremo il lavoro con le frazioni che hanno una forma irregolare o con frazioni per le quali è possibile un’ulteriore semplificazione.
Se qualche procedura o esempio ti crea problemi, sentiti libero di scrivere la tua opinione o domanda utilizzando il modulo di commento in fondo a questa pagina. Siamo sempre disponibili ad offrire ulteriore assistenza ai nostri lettori. Grazie!
Tags: Come, Esempio, Frazioni, Intero, Moltiplicazione, Numero, Problema, Tra

 Attendere prego...
Attendere prego...