In questo testo puoi vedere una rappresentazione della fattorizzazione in fattori primi dei numeri da 1 a 100! Sebbene a prima vista la procedura sia molto semplice, la procedura è estremamente importante. Usarlo correttamente in futuro ti aiuterà ad apprendere abilità matematiche molto più complesse! Se sai come eseguire correttamente la fattorizzazione in fattori primi in di un numero nei suoi multipli primi, sarai ovviamente in grado di risolvere problemi matematici più complessi con l’aiuto di trucchi matematici e procedure abbreviate. Dai un’occhiata al nostro contenuto testuale qui sotto!
- Regola della fattorizzazione prima
- Molti esempi con fattorizzazione in fattori primi utilizzando rami di fattori.
- Tabella della fattorizzazione in fattori primi dei numeri da 1 a 100.
- Molti esempi video progettati per facilitare l’adattamento alla scomposizione in fattori primi.
Iniziamo con:
Regola della fattorizzazione in fattori primi
Logicamente, innanzitutto, prima di iniziare la divisione pratica dei fattori primi, è necessario definire cos’è un numero primo e cos’è un numero complesso! Facciamo esattamente questo prima!
- Un numero primo è qualsiasi numero divisibile solo per se stesso e per il numero 1 senza lasciare resto. Quando dividi un numero primo con un altro numero, ottieni sempre il resto!
- Un numero complesso è qualsiasi numero divisibile per 1, per se stesso e per almeno un altro numero senza lasciare resto.
Il prerequisito principale per avviare la procedura è soddisfatto. Quando si sa già bene cos’è un numero primo e cos’è un numero complesso, possiamo definire la regola per la scomposizione in fattori primi. È fatto proprio qui sotto!
Un numero può essere diviso in diversi multipli purché tutti i suoi multipli non siano primi. Allo stesso tempo, non è affatto importante secondo quale regola esatta verrà eseguita la divisione. Dobbiamo solo dividere ogni multiplo diverso finché non li portiamo tutti a un numero primo.
Di seguito puoi vedere alcuni esempi concreti in cui viene eseguita la fattorizzazione in fattori primi!
Esempi di fattorizzazione in fattori primi:
Esempi
Esempio 1: scomponi il numero 10 in fattori primi!
Se iniziamo a dividere il numero 10, è facile vedere che è più semplice rappresentarlo come il prodotto dei numeri 2 e 5. I numeri 2 e 5 sono numeri primi, quindi la divisione è immediatamente completa. Graficamente, la scomposizione del numero 10 è presentata nell’immagine qui sotto!
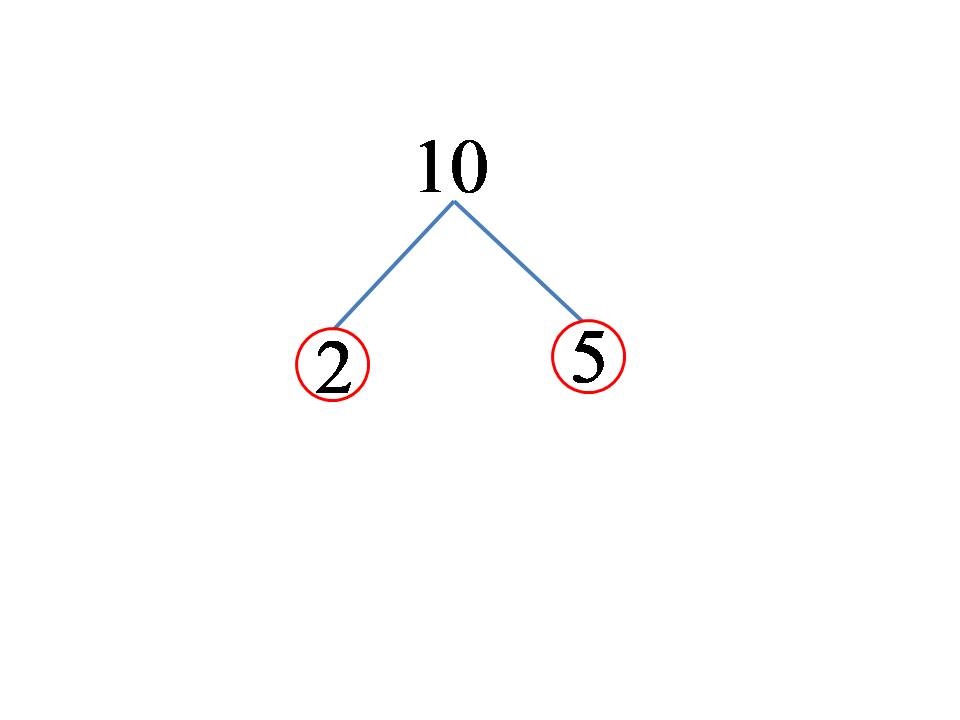
Il numero 10, dopo la suddivisione nei suoi multipli primi, può essere scritto nella seguente forma:
10 = 2×5
Esempio 2: scomponi il numero 12 in fattori primi!
Iniziamo a dividere il numero 12! Una possibilità è dividerlo nel prodotto dei numeri 3 e 4. Il numero 3 è primo, ma il numero complesso 4 dobbiamo continuare a dividerlo. Dividiamo 4 nel prodotto dei numeri 2 e 2. Graficamente, la scomposizione del numero 12 è presentata nella figura qui sotto!
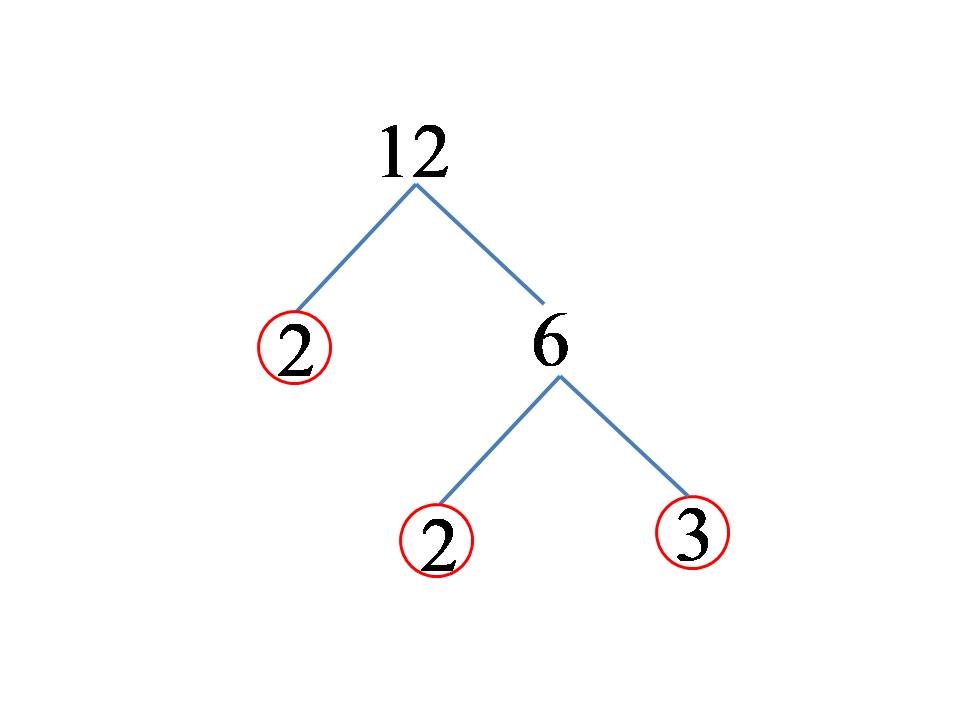
Il numero 12, dopo la fattorizzazione in fattori primi, può essere scritto nella seguente forma:
12 = 2×2×3
Tabella di fattorizzazione dei numeri primi da 1 a 100
La tabella disponibile di seguito contiene tutti i numeri da 1 a 100. In essa puoi vedere i dati su quali numeri da 1 a 100 sono numeri primi. Inoltre, qui, la tabella presenta la scomposizione in fattori primi di tutti i numeri complessi da 1 a 100 nei loro fattori primi.
| Numero | Fattorizzazione (Se è possibile) |
|---|---|
| 1 | Numero primo |
| 2 | Numero primo |
| 3 | Numero primo |
| 4 | 4 = 2 x 2 |
| 5 | Numero primo |
| 6 | 6 = 2 x 3 |
| 7 | Numero primo |
| 8 | 8 = 2 x 2 x 2 |
| 9 | 9 = 3 x 3 |
| 10 | 10 = 2 x 5 |
| 11 | Numero primo |
| 12 | 12 = 2 x 2 x 3 |
| 13 | Numero primo |
| 14 | 14 = 2 x 7 |
| 15 | 15 = 3 x 5 |
| 16 | 16 = 2 x 2 x 2 x 2 |
| 17 | Numero primo |
| 18 | 18 = 2 x 3 x 3 |
| 19 | Numero primo |
| 20 | 20 = 2 x 2 x 5 |
| 21 | 21 = 3 x 7 |
| 22 | 22 = 2 x 11 |
| 23 | Numero primo |
| 24 | 24 = 2 x 2 x 2 x 3 |
| 25 | 25 = 5 x 5 |
| 26 | 26 = 2 x 13 |
| 27 | 27 = 3 x 3 x 3 |
| 28 | 28 = 2 x 2 x 7 |
| 29 | Numero primo |
| 30 | 30 = 2 x 3 x 5 |
| 31 | Numero primo |
| 32 | 32 = 2 x 2 x 2 x 2 x 2 |
| 33 | 33 = 3 x 11 |
| 34 | 34 = 2 x 17 |
| 35 | 35 = 5 x 7 |
| 36 | 36 = 2 x 2 x 3 x 3 |
| 37 | Numero primo |
| 38 | 38 = 2 x 19 |
| 39 | 39 = 3 x 13 |
| 40 | 40 = 2 x 2 x 2 x 5 |
| 41 | Numero primo |
| 42 | 42 = 2 x 3 x 7 |
| 43 | Numero primo |
| 44 | 44 = 2 x 2 x 11 |
| 45 | 45 = 3 x 3 x 5 |
| 46 | 46 = 2 x 23 |
| 47 | Numero primo |
| 48 | 48 = 2 x 2 x 2 x 2 x 3 |
| 49 | 49 = 7 x 7 |
| 50 | 50 = 2 x 5 x 5 |
| 51 | 51 = 3 x 17 |
| 52 | 52 = 2 x 2 x 13 |
| 53 | Numero primo |
| 54 | 54 = 2 x 3 x 3 x 3 |
| 55 | 55 = 5 x 11 |
| 56 | 56 = 2 x 2 x 2 x 7 |
| 57 | 57 = 3 x 19 |
| 58 | 58 = 2 x 29 |
| 59 | Numero primo |
| 60 | 60 = 2 x 2 x 3 x 5 |
| 61 | Numero primo |
| 62 | 62 = 2 x 31 |
| 63 | 63 = 3 x 3 x 7 |
| 64 | 64 = 2 x 2 x 2 x 2 x 2 x 2 |
| 65 | 65 = 5 x 13 |
| 66 | 66 = 2 x 3 x 11 |
| 67 | Numero primo |
| 68 | 68 = 2 x 2 x 17 |
| 69 | 69 = 3 x 23 |
| 70 | 70 = 2 x 5 x 7 |
| 71 | Numero primo |
| 72 | 72 = 2 x 2 x 2 x 3 x 3 |
| 73 | Numero primo |
| 74 | 74 = 2 x 37 |
| 75 | 75 = 3 x 5 x 5 |
| 76 | 76 = 2 x 2 x 19 |
| 77 | 77 = 7 x 11 |
| 78 | 78 = 2 x 3 x 13 |
| 79 | Numero primo |
| 80 | 80 = 2 x 2 x 2 x 2 x 5 |
| 81 | 81 = 3 x 3 x 3 x 3 |
| 82 | 82 = 2 x 41 |
| 83 | Numero primo |
| 84 | 84 = 2 x 2 x 3 x 7 |
| 85 | 85 = 5 x 17 |
| 86 | 86 = 2 x 43 |
| 87 | 87 = 3 x 29 |
| 88 | 88 = 2 x 2 x 2 x 11 |
| 89 | Numero primo |
| 90 | 90 = 2 x 3 x 3 x 5 |
| 91 | 91 = 7 x 13 |
| 92 | 92 = 2 x 2 x 23 |
| 93 | 93 = 3 x 31 |
| 94 | 94 = 2 x 47 |
| 95 | 95 = 5 x 19 |
| 96 | 96 = 2 x 2 x 2 x 2 x 2 x 3 |
| 97 | Numero primo |
| 98 | 98 = 2 x 7 x 7 |
| 99 | 99 = 3 x 3 x 11 |
| 100 | 100 = 2 x 2 x 5 x 5 |
| 101 | Numero primo |
Esempi video
Si consiglia di guardare il video che contiene tutti gli esempi con la fattorizzazione in fattori primi da 1 a 25. Nel video hai la possibilità di vedere come avviene la divisione passo dopo passo utilizzando la metodologia della rappresentazione per rami di multipli.
Tags: Fattori, Fattorizzazione, Numeri, Primi
 Attendere prego...
Attendere prego...