Cos’è un’equazione quadratica? Come si possono determinare le soluzioni di un’equazione di secondo grado? Qual è la formula che può essere utilizzata per calcolare la soluzione di un’equazione di secondo grado? Nella continuazione di questo luogo puoi trovare le risposte corrette a queste domande. Di seguito ti consentiremo di vedere esempi completamente risolti in cui la soluzione di una particolare equazione di secondo grado è praticamente determinata.
Ciascuno dei nostri lettori può accedere a materiale video contenente un numero enorme di esempi risolti che ti aiuteranno a risolvere in modo permanente il problema delle equazioni quadratiche. Rimani qui per qualche minuto per aiutarti a risolvere questo problema di matematica.
Cos’è un’equazione quadratica
L’equazione che ha la forma:
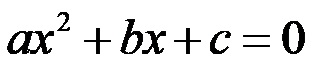
dove a è diverso da zero, mentre a, b e c sono coefficienti reali si chiama equazione di secondo grado!
Se tutti e tre i coefficienti sono diversi da zero, allora diciamo che l’equazione quadratica è un’equazione quadratica completa o completa!
Se uno dei coefficienti boc è uguale a zero (o entrambi sono contemporaneamente uguali a zero), allora l’equazione quadratica si dice che sia un’equazione quadratica incompleta.
Ogni equazione quadratica può avere una o due soluzioni!
La formula per determinare la soluzione o le soluzioni di un’equazione di secondo grado completa è:
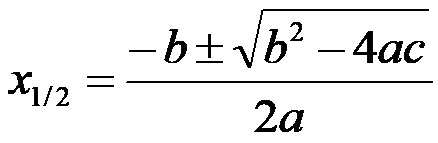
I tre coefficienti dovrebbero essere utilizzati per determinare la soluzione. È facile commettere un errore nell’individuare i tre coefficienti. Per evitare errori, è necessario prestare attenzione se l’equazione quadratica è nella forma generale o meno. Se non è nella forma generale, bisogna prima trasformare l’equazione quadratica nella forma generale per accertare con precisione quale sia il valore dei tre coefficienti.
Non appena vengono rilevati i tre coefficienti, il loro valore viene inserito nella formula sopra, dopo di che vengono determinate le soluzioni dell’equazione quadratica.
Di seguito puoi vedere come vengono calcolate le soluzioni di una specifica equazione di secondo grado!
Come determinare le soluzioni di un’equazione quadratica
Guarda come vengono determinate le soluzioni dell’equazione quadratica nell’esempio seguente!
Esempio 1. Determina le soluzioni dell’equazione di secondo grado riportata nella figura seguente!
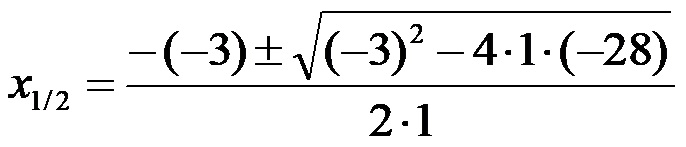
L’equazione quadratica dell’esempio sopra ha coefficienti a = 1, b = -3 e – 28! Se nella formula di calcolo si inserisce il valore di questi coefficienti si ottiene la seguente espressione:
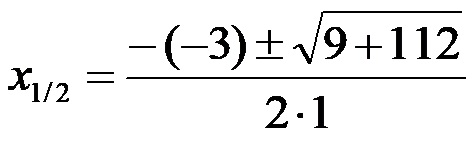
Nel passaggio successivo calcoliamo il quadrato all’interno dell’espressione radice. Quindi otteniamo:
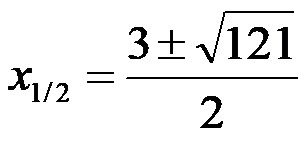
Nel passaggio successivo, calcoliamo il prodotto dei numeri sotto l’espressione radice, dopodiché otteniamo:
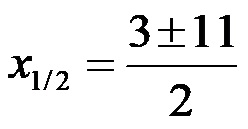
Adesso facciamo il radice!
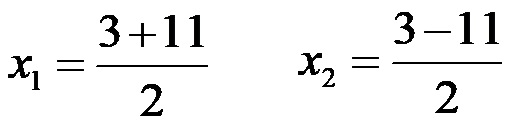
Infine, quando si calcola la prima soluzione, si scrive il segno +, mentre quando si calcola la seconda soluzione si scrive il segno -. La formazione di entrambe le soluzioni è simile all’immagine qui sotto!
Al numeratore della prima soluzione aggiungiamo, mentre al numeratore della seconda soluzione sottraiamo, dopodiché otteniamo:
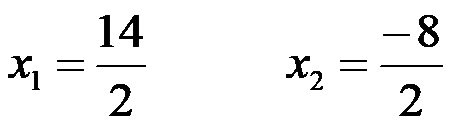
Dopo la divisione otteniamo le due soluzioni -4 e 7!
Come puoi vedere, determinare le soluzioni di un’equazione di secondo grado non è affatto una procedura matematica difficile, ma a causa della lunghezza della soluzione, devi fare attenzione a non commettere un piccolo errore, che potrebbe portare a soluzioni sbagliate!
In questi problemi di matematica è sempre bello verificare le soluzioni. Se al posto di x nell’equazione quadratica in due diverse situazioni sostituiamo il valore delle soluzioni e otteniamo un’equazione esatta, allora possiamo essere convinti di aver risolto correttamente l’equazione di secondo grado.
Verifica della soluzione
Controlliamo se le due soluzioni che abbiamo ottenuto utilizzando la formula sono realmente corrette. Inizieremo esaminando la prima soluzione, ovvero al posto di x nell’equazione di secondo grado inseriremo -4! Dopo aver inserito questa soluzione, l’espressione assume la forma seguente:
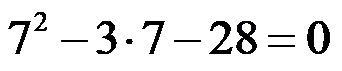
Continuiamo la risoluzione, dove all’inizio calcoliamo la quadratura, dopodiché otteniamo:
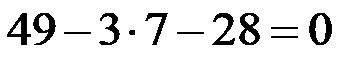
Quindi calcoliamo il prodotto!
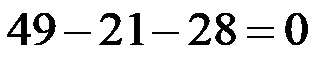
Alla fine, sommando e sottraendo, otteniamo la soluzione corretta (49-49=0)!
Ripetiamo la stessa procedura con la seconda soluzione. Ora al posto della x inseriamo la seconda soluzione, ovvero il numero 7. L’espressione risultante è riportata nella figura qui sotto!
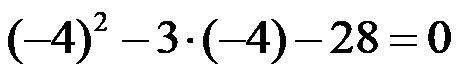
Ripetiamo la procedura di soluzione che abbiamo appena completato per la prima soluzione, quindi ricominciamo a quadrare.
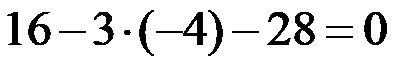
Calcoliamo il prodotto.
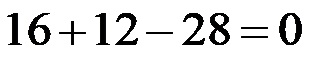
Aggiungendo e sottraendo, troviamo che anche la seconda soluzione è corretta perché otteniamo nuovamente un’equazione esatta (28-28=0)!
In questo modo possiamo affermare con sicurezza che i numeri -4 e 7 sono effettivamente soluzioni dell’equazione di secondo grado! Ti consigliamo di eseguire questo tipo di controllo per ogni attività risolta, perché è questo tipo di cautela che un giorno potrà aiutarti a trovare il tuo errore e correggerlo in modo tempestivo!
Esempi video
Il materiale video seguente contiene molte informazioni sull’equazione di secondo grado ed esempi in cui vengono calcolate le soluzioni dell’equazione quadratica. Usando il video puoi vedere che il tipo di soluzione o soluzioni di un’equazione di secondo grado dipende solo dall’espressione della radice o dal discriminante dell’equazione quadratica!
In una guida separata sul nostro sito web potete scoprire come vengono calcolate le soluzioni di un’equazione quadratica che non è completa!
Tags: Equazione, Esempi, Quadratica, Soluzione
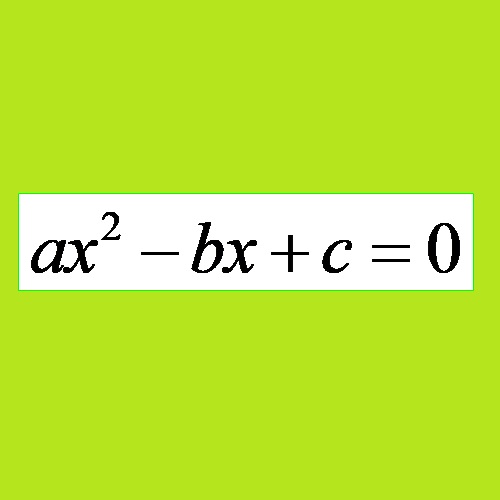
 Attendere prego...
Attendere prego...