Cos’è un’equazione lineare? Quali metodi vengono utilizzati per determinare la soluzione esatta di un’equazione lineare? In che modo, in uno specifico esempio di vita reale, è possibile utilizzare per risolvere un problema? Puoi trovare la risposta alle domande precedenti su questo sito qui sotto! Qui spiegheremo tutto ciò che sappiamo, come creare e come determinarne la soluzione! Di seguito in questa pagina puoi confrontare diversi metodi per risolvere! In questo testo ci concentreremo sulle equazioni lineari con un’incognita e in futuro creeremo contenuti speciali per altri tipi!
Cos’è un’equazione lineare con un’incognita
L’equazione riportata nella figura seguente:
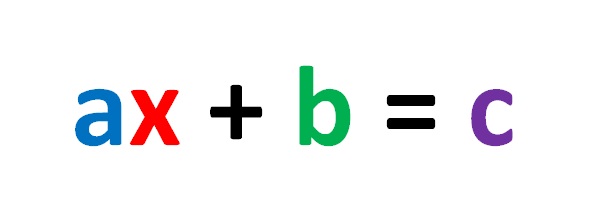
In cui i numeri a, b e c sono numeri reali e a non è uguale a zero, si parla di equazione lineare ad una incognita!
Una soluzione a un’equazione lineare è un numero che sostituiremo al posto di x e calcoleremo, otteniamo un’equazione esatta!
Sotto la figura ci sono tre diverse equazioni lineari con un’incognita!
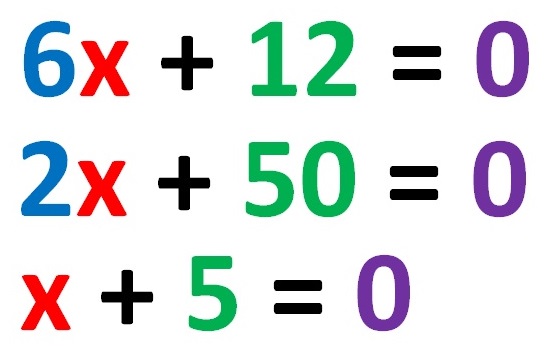
Risoluzione di un’equazione lineare
Proviamo a determinare una soluzione a un’equazione lineare! Guarda l’esempio qui sotto!
Esempio 1. Calcola la soluzione dell’equazione lineare nella figura qui sotto!

Quando risolviamo, il nostro obiettivo è che l’incognita x rimanga da sola sul lato sinistro dell’equazione, mentre trasferiamo tutti i valori noti sul lato destro dell’equazione!
Per eliminare il numero -14 sul lato sinistro, aggiungeremo +14 contemporaneamente su entrambi i lati dell’equazione! L’espressione è simile alla seguente:
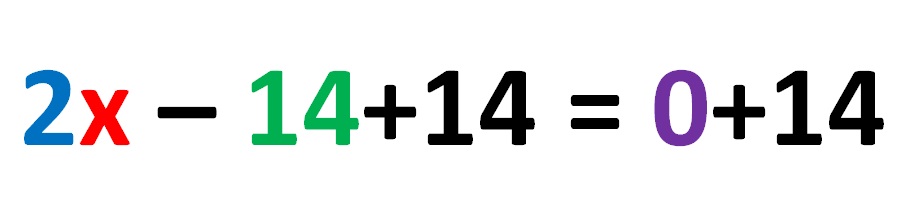
Dopo aver calcolato le operazioni matematiche appropriate su entrambi i lati sinistro e destro dell’equazione lineare, otteniamo:
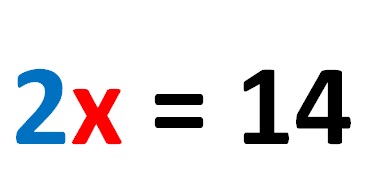
Il numero 2 che si trova ancora sul lato sinistro dell’equazione lineare può essere rimosso solo se entrambi i lati sono divisi per il numero 2. Facciamolo! L’espressione assume la forma seguente:
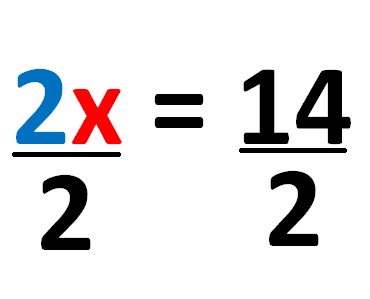
Dopo aver diviso entrambi i membri per il numero 2, otteniamo:
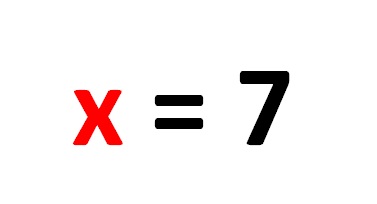
È più che chiaro che l’ultimo passaggio ci offre la soluzione dell’equazione lineare x=7!
Verifica della soluzione di un’equazione lineare con un’incognita
Per essere sicuri che la soluzione ottenuta risolvendo sia reale, è sufficiente sostituire la soluzione ottenuta al posto di x nell’equazione lineare e calcolare se otterremo un’equazione esatta.
Per prima cosa sostituiamo il valore risultante al posto di x!

Successivamente si calcola il prodotto dei due numeri, dopo di che si ottiene l’espressione:

Poiché 14-14=0 è effettivamente un’equazione esatta, traiamo la conclusione che il numero 7 è effettivamente una soluzione esatta!
Creazione
Oltre a risolvere correttamente, è molto importante essere in grado di creare in una situazione del mondo reale e risolvere un particolare problema di matematica risolvendolo! Di seguito ti proporremo una situazione concreta in cui possiamo utilizzare come possibile soluzione ad un vero problema di matematica!
Esempio 2. Un rettangolo ha il perimetro di 40 metri! La lunghezza del rettangolo è 10 metri maggiore della sua larghezza. Qual è la lunghezza dei lati del rettangolo?
Naturalmente, per risolvere un esempio del genere è necessario conoscere la formula per calcolare il perimetro di un rettangolo! Clicca sul testo colorato nella frase precedente per ricordare come calcolare il perimetro di un rettangolo se ne hai bisogno!
Dalle informazioni fornite sul rettangolo, dobbiamo prima creare un’immagine che ne descriva le caratteristiche! L’immagine potrebbe assomigliare a questa:
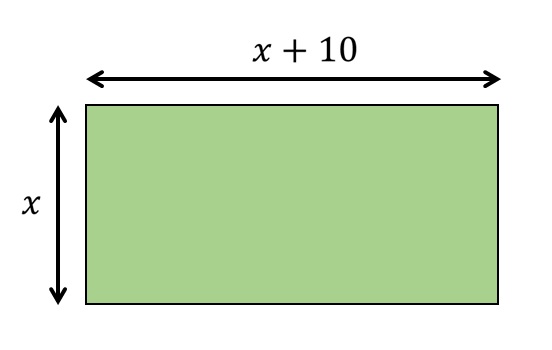
Applicando la regola per determinare il perimetro di un rettangolo si ottiene la seguente espressione!
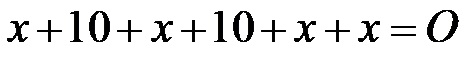
Innanzitutto, sul lato sinistro, raccoglieremo tutti i termini che contengono x, e separatamente raccoglieremo tutti quelli che non contengono x. Allo stesso tempo, inseriremo 40 metri nel posto per il valore del perimetro! L’espressione assume la forma seguente:
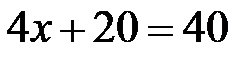
Sottraiamo 20 da entrambi i lati dell’equazione lineare, dopodiché l’equazione assume la seguente forma:
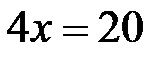
Infine, dividiamo entrambi i membri dell’equazione per il numero 4, dopodiché otteniamo la soluzione finale per la lunghezza di x!
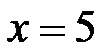
Infine, dobbiamo utilizzare il valore ottenuto per x risolvendo l’equazione lineare per determinare la lunghezza dei lati del rettangolo! La larghezza del rettangolo è di 5 metri, mentre la sua lunghezza è di 15 metri, il che soddisfa la condizione che la lunghezza sia 10 metri maggiore della larghezza, e allo stesso tempo la seconda condizione affinché il perimetro sia di 40 metri!
Esempi
Il materiale video in fondo a questa pagina web contiene un numero enorme di esempi di equazioni lineari risolte! Inoltre, il video ti aiuterà sicuramente a imparare come creare in una situazione reale e ad usarla per risolvere un problema di matematica! Ti consigliamo di guardare tutto il video e di fare molta pipì! Buona fortuna!
Tags: Equazione, Esempi, Formula, Incognita, Lineare, Problema
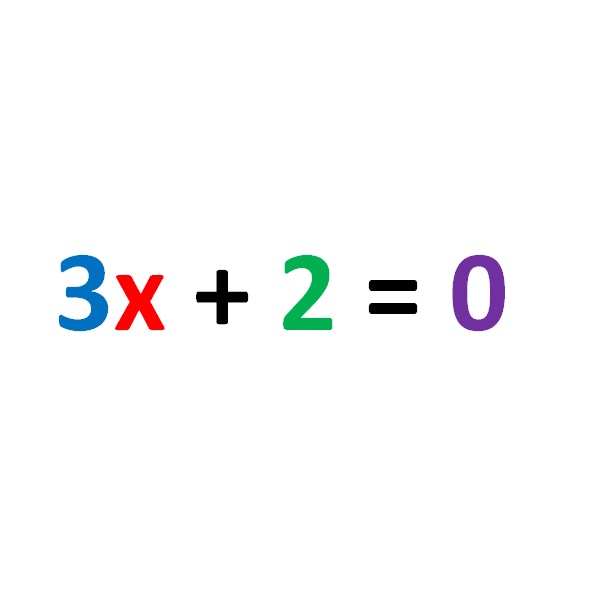
 Attendere prego...
Attendere prego...