Cos’è quel cerchio trigonometrico? A cosa serve quel cerchio trigonometrico? Il nome stesso del cerchio trigonometrico non ci associa alla trigonometria! Sì, la tua ipotesi è corretta!
Il cerchio trigonometrico viene utilizzato per una definizione più semplice delle funzioni trigonometriche, ma anche per la lettura diretta e la determinazione del valore delle funzioni trigonometriche da alcuni angoli caratteristici di uso frequente, come gli angoli con 30, 45, 60, 90, 120, 135, ecc. gradi.
È il raggio del cerchio trigonometrico che ha lunghezza 1 in combinazione con le regole per definire le funzioni trigonometriche con un triangolo rettangolo che viene utilizzato per semplificare il modo di apprendere e comprendere il valore delle funzioni trigonometriche di angoli di dimensione caratteristica. Di seguito in questa pagina spiegheremo tutto sul cerchio trigonometrico, ma anche molte altre informazioni aggiuntive ad esso direttamente o indirettamente correlate!
Tutto sul cerchio trigonometrico
Per cominciare vi suggeriamo di dare una buona occhiata al video qui sotto. Considera attentamente tutti i dettagli in esso contenuti per imparare:
- Quali conoscenze preliminari sono necessarie per capire come utilizzare il cerchio trigonometrico?
- Come definire e leggere i valori dal cerchio trigonometrico.
- Come formare una tabella con i valori più comunemente utilizzati delle funzioni trigonometriche da angoli caratteristici.
Tabella dei valori ottenuti con un cerchio trigonometrico
Se hai esaminato attentamente e compreso il contenuto del materiale video sopra, probabilmente avrai alcune domande aggiuntive relative a come ottenere i valori delle funzioni trigonometriche utilizzando un cerchio trigonometrico! In questa sezione, esaminiamo diverse situazioni che descriveremo sia in radianti che in gradi.
Esempio 1. Valore delle funzioni trigonometriche da un angolo di 30 gradi!
Per prima cosa, guardiamo l’immagine che descrive come un angolo di 30 gradi esatti possa essere considerato utilizzando un cerchio trigonometrico.
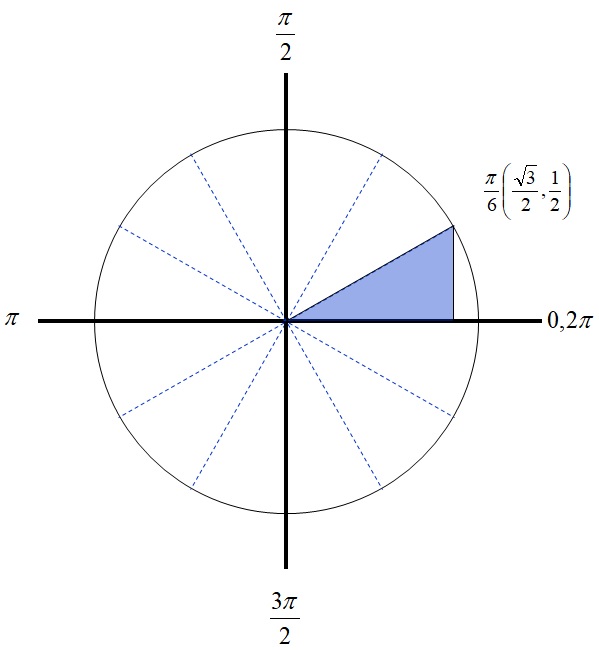
Dall’immagine si può vedere che le coordinate stesse sono le lunghezze dei due cateti del triangolo rettangolo, mentre la sua ipotenusa è identica al raggio del cerchio trigonometrico ed è uguale a 1. Per un angolo di 30 gradi, la coordinata y mostra la dimensione del lato opposto, mentre la coordinata x mostra la lunghezza del lato adiacente. Pertanto (secondo la definizione di funzioni trigonometriche), i valori delle funzioni trigonometriche per l’angolo di 30 gradi sono:
Seno di 30:
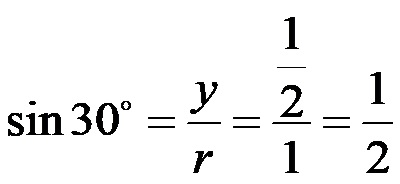
Coseno di 30:
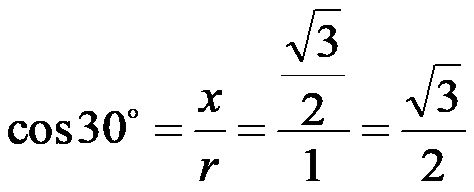
Tangente di 30:
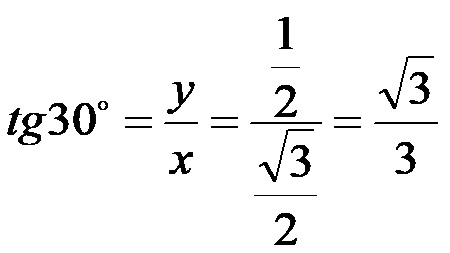
Cotangente di 30:
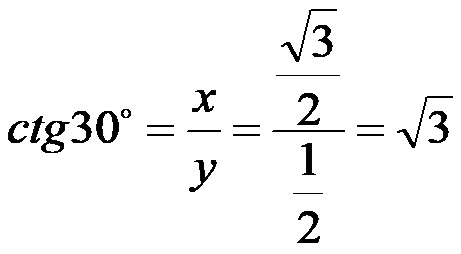
Esempio 2. Valore delle funzioni trigonometriche da un angolo di 45 gradi!
Per prima cosa, diamo un’occhiata all’immagine che descrive come un angolo di esattamente 45 gradi può essere considerato utilizzando un cerchio trigonometrico.
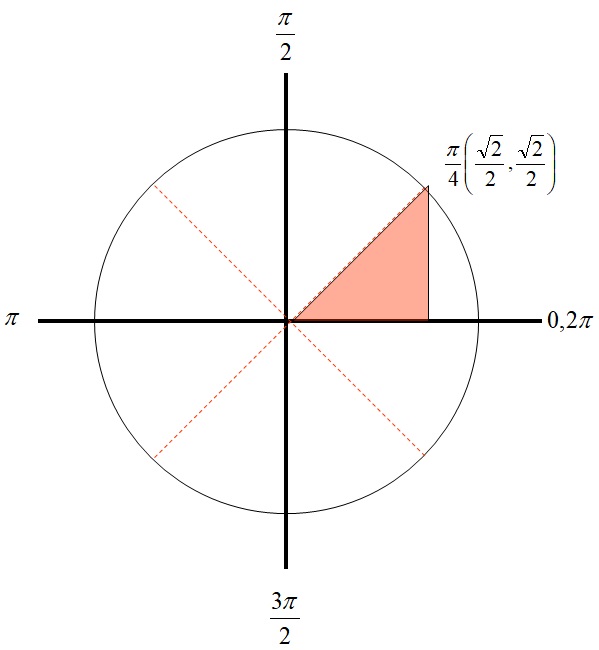
Secondo la definizione di funzioni trigonometriche e le regole che abbiamo già utilizzato nell’esempio precedente, è facile comprendere che i valori delle funzioni trigonometriche dell’angolo di 45 gradi sono:
Seno di 45:
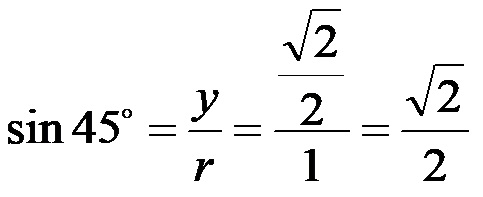
Coseno di 45:
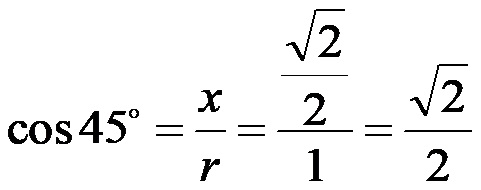
Tangente di 45:
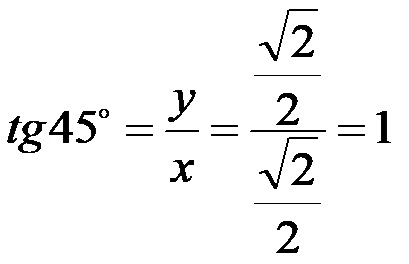
Cotangente di 45:
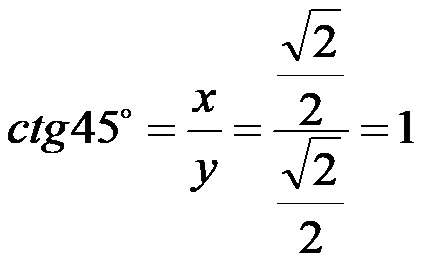
Tabella dei valori
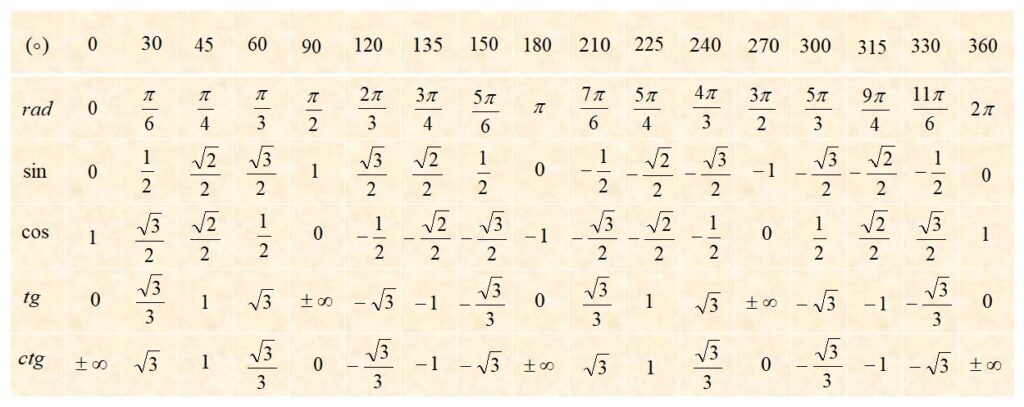
La tabella seguente contiene i valori delle funzioni trigonometriche degli angoli caratteristici ottenuti utilizzando un cerchio trigonometrico!
Puoi utilizzare i due esempi sopra per confrontare i risultati di tutti gli altri angoli distintivi nel video!
Semplicemente, se non hai capito qualcosa la prima volta, ti suggeriamo di tornare ancora una volta e con le nuove conoscenze, riprovare e assicurarti che ora guarderai le stesse cose nel modo giusto! Buona fortuna!
Tags: 120, 135, 30, 45, 60, 90, Cerchio, Gradi, Radianti, Trigonometrico
 Attendere prego...
Attendere prego...