Addizione e sottrazione di radici nel modo giusto! Qui vedrai come addizione e sottrarre le radici, tanti esempi e compiti risolti! La procedura più importante relativa a queste operazioni matematiche con le radici è che ognuno dovrebbe essere in grado di eseguire un’opportuna semplificazione delle radici (solo se possibile), per capire se le radici date possono o meno essere addizione o sottrazione.
La stessa procedura di addizione e sottrazione di radici è molto semplice, la parte più problematica è capire se le radici date hanno o meno la stessa espressione di radice. La conclusione è la seguente:
l’addizione e la sottrazione di radici è possibile solo se due (o se raccogliamo più radici) radici hanno un’espressione di radice identica. Se la loro espressione di radice è diversa, non è possibile sommare e sottrarre tre radici!
Come addizione e sottrazione radici
Addizione e sottrarre radici si riduce ad aggiungere e sottrarre i fattori che precedono l’espressione della radice. Così facendo, semplicemente, l’espressione della radice rimane la stessa (non la cambiamo affatto), e le operazioni matematiche valgono solo per i moltiplicatori. Se addizione le radici, calcoliamo la loro somma, mentre se le sottraiamo, calcoliamo la loro differenza.
Addizione delle radici
Vediamo prima due esempi con l’aggiunta di radici!
Esempio 1. Calcola la somma delle radici dell’immagine qui sotto!
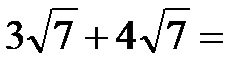
Come abbiamo già accennato in precedenza nel testo, l’espressione della radice rimane invariata e vengono aggiunti i moltiplicatori che si trovano davanti alla radice! Pertanto la somma delle radici è:
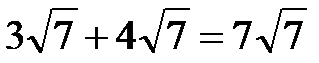
Esempio 2. Calcola la somma delle radici dell’immagine qui sotto!
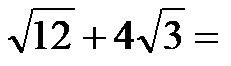
Ovviamente, a prima vista, l’espressione radicale delle radici è diversa, o almeno così sembra. In queste situazioni, dobbiamo scoprire se una o entrambe le radici possono essere semplificate, per capire se possiamo aggiungerle o meno! Possiamo rappresentare il numero 12 come il prodotto tra i numeri 4 e 3, e poiché la radice di 4 è il numero 2, possiamo estrarre il 2 prima della radice come moltiplicatore, mentre sotto la radice rimarrà solo il numero 3.
In quella situazione, dopo aver semplificato la prima radice, si vede che entrambe le radici hanno la stessa espressione di radice. Adesso è facile rendersi conto che possiamo raccogliere le radici. L’intera soluzione è riportata nell’immagine qui sotto!
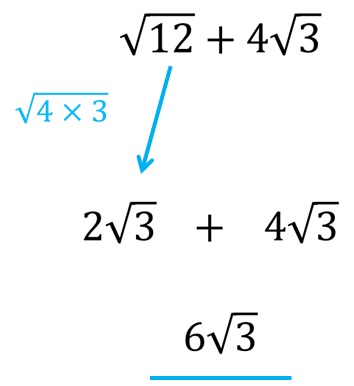
Sottrazione radici
Ora tocca a noi vedere due esempi con il radice!
Esempio 3. Calcola la differenza tra le radici indicate nell’immagine qui sotto!
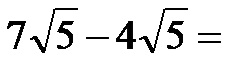
Ovviamente le radici nell’immagine sopra hanno la stessa espressione di radice quindi è molto semplice sottrarle l’una dall’altra. In poche parole, l’espressione della radice rimane invariata, mentre sottraiamo i moltiplicatori. È facile vedere che la soluzione è:
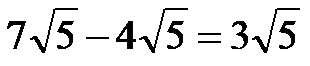
Esempio 4. Calcola la differenza tra le radici dell’immagine qui sotto!
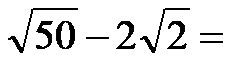
Ancora una volta, proprio come nel secondo esempio sopra, non abbiamo un’idea chiara se le radici nell’immagine sopra abbiano o meno le stesse espressioni di radice. Innanzitutto proviamo a semplificare!
Possiamo rappresentare il numero 50 come un prodotto tra i numeri 25 e 2, e poiché la radice di 25 è il numero 5, possiamo estrarre il 5 prima della radice come moltiplicatore, mentre sotto la radice rimarrà solo il numero 2 Ora è già chiaro che queste due radici hanno la stessa espressione di radice e possiamo sottrarle.
L’intera procedura per determinare la differenza tra le due radici è riportata nella figura seguente!
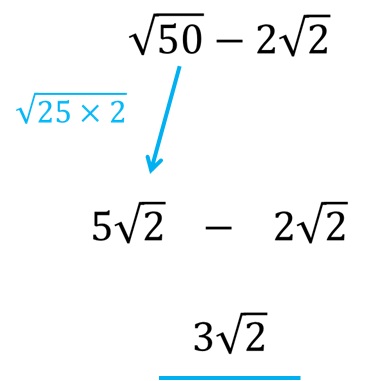
Esempi video
Lasciati immergere nella varietà di esempi contenuti nel video qui sotto! Un’abbondanza di esempi con addizione e sottrazione di radici ti aiuterà a imparare molti trucchi matematici nella ricerca di una soluzione. Ti consigliamo di controllarli tutti! Buona fortuna!
Tags: Addizione, Addizione e sottrazione, Esempi, Esempio, Problema, Radici, Sottrazione
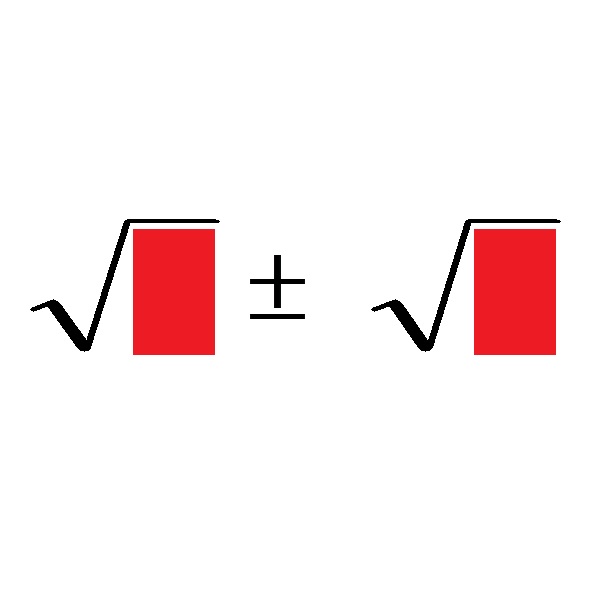
 Attendere prego...
Attendere prego...