Funzioni trigonometriche e loro definizione utilizzando un triangolo rettangolo! Su questo sito web puoi accedere a un modo unico per definire le funzioni trigonometriche seno, coseno, tangente e cotangente utilizzando un triangolo rettangolo. Di seguito nel testo e nel video avete tutte le informazioni necessarie presentate in modo adeguato per aiutarvi a comprendere questo problema in modo da impostare una buona conoscenza di base affinché possiate comprendere ulteriormente tutti i segreti della trigonometria!
Passo dopo passo ti aiuteremo a capire cosa sono effettivamente le funzioni trigonometriche, come vengono definite e come vengono utilizzate in uno specifico problema di matematica per calcolare alcuni valori sconosciuti in un triangolo rettangolo!
Definizione di funzioni trigonometriche
Per definire le quattro funzioni di cui sopra utilizzeremo un triangolo rettangolo per il suo angolo situato nel vertice B. L’angolo beta ci servirà per definire seno, coseno, tangente e cotangente come funzioni trigonometriche di base! Di seguito è riportata l’immagine di un triangolo rettangolo e i nomi dei suoi lati in termini di come sono posizionati rispetto all’angolo beta!
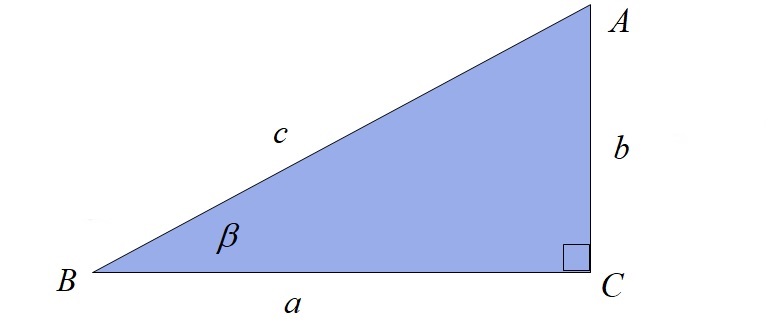
Dalla figura si vede che il lato del rettangolo che non tocca l’angolo beta si chiama lato opposto, mentre il lato che, oltre all’ipotenusa, forma l’angolo beta si dice adiacente. Ciò conferisce ai due lati un nome speciale in termini di posizione rispetto all’angolo beta. Logicamente, l’ipotenusa (il lato più lungo in un triangolo rettangolo) mantiene il proprio nome. Sono questi i nomi che useremo in seguito per definire le funzioni trigonometriche seno, coseno, tangente e cotangente beta!
Il seno di beta è il quoziente del cateto opposto e dell’ipotenusa! La formula per il seno beta è:
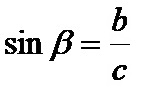
Il coseno di beta è il quoziente del cateto adiacente e dell’ipotenusa! La formula per il coseno beta è:
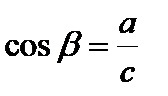
La tangente di beta è il quoziente tra il cateto opposto e il cateto adiacente! La formula per la tangente beta è:
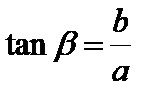
La cotangente beta è il quoziente tra il cateto adiacente e il cateto opposto! La formula per la cotangente beta è:
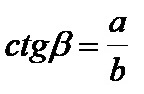
*Le formule per le funzioni trigonometriche per l’angolo situato nel vertice A del triangolo rettangolo saranno completamente diverse, perché i lati del triangolo rettangolo in quel caso vanno visti rispetto al vertice A. In quella situazione i termini opposti e la gamba adiacente avranno un significato abbastanza diverso, quindi in quel caso saranno lati diversi dal nostro punto di vista dal vertice B e dall’angolo beta!
Lettura delle funzioni trigonometriche da un triangolo rettangolo
Impariamo a leggere le funzioni trigonometriche da un triangolo rettangolo i cui lati hanno lunghezza nota! Guarda l’esempio qui sotto!
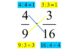
Esempio 1. Quali frazioni descrivono tutte e quattro le funzioni trigonometriche per gli angoli alfa e beta nel triangolo rettangolo indicato nella figura seguente?
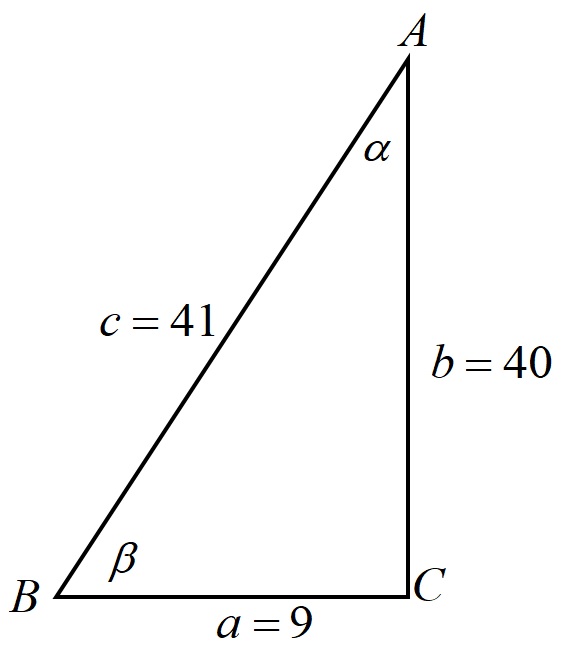
Cominciamo prima con le funzioni trigonometriche per l’angolo alfa! Per questo angolo, il lato opposto ha una lunghezza di 9 cm e il lato adiacente ha una lunghezza di 40 cm. Conoscendo la posizione rispetto ai lati leggiamo le funzioni trigonometriche per questo angolo!
Il seno alfa è il quoziente del cateto opposto di 9 cm e dell’ipotenusa di 41 cm. La formula è:
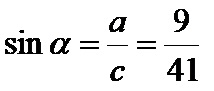
Il coseno alfa è il quoziente del cateto adiacente di 40 cm e dell’ipotenusa di 41 cm. La formula è:
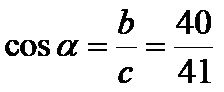
La tangente alfa è il quoziente tra il cateto opposto di 9 cm e il cateto adiacente di 40 cm. La formula è:
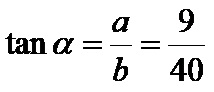
La cotangente alfa è il quoziente tra il cateto adiacente di 40 cm e il cateto opposto di 9 cm. La formula è:
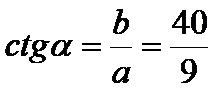
Vediamo ora come stanno le cose in termini di angolo beta! In relazione a questo angolo, la gamba opposta è il lato che misura 40 cm, e la gamba adiacente è il lato che misura 9 cm! Una volta confermato il posizionamento dei lati rispetto all’angolo beta, resta da leggere bene le funzioni trigonometriche!
Il seno beta è il quoziente del cateto opposto di 40 cm e dell’ipotenusa di 41 cm. La formula è:
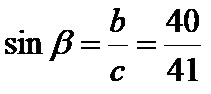
Il coseno beta è il prodotto del cateto adiacente di 9 cm e dell’ipotenusa di 41 cm. La formula è:
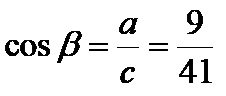
La tangente beta è il quoziente tra il cateto opposto di 40 cm e il cateto adiacente di 9 cm. La formula è:
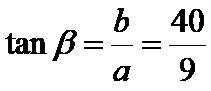
La cotangente beta è il quoziente tra il cateto adiacente di 9 cm e il cateto opposto di 40 cm. La formula è:
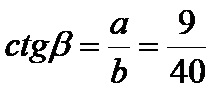
Come si può facilmente vedere dall’esempio risolto sopra, non è affatto difficile leggere correttamente i valori delle funzioni trigonometriche da un triangolo rettangolo di cui si conoscono le lunghezze di tutti e tre i lati.
Applicazione delle funzioni trigonometriche ai problemi
Le funzioni trigonometriche seno, coseno, tangente e cotangente possono essere applicate a semplici problemi di matematica in cui devono essere determinati i valori dei lati o degli angoli in un triangolo rettangolo. Un esempio di problemi matematici di questo tipo è contenuto nel video qui sotto! Ti consigliamo di prestare attenzione a tutti gli esempi nel video perché questi esempi possono aiutarti a imparare molto!
Le funzioni trigonometriche sono una parte problematica della matematica per molti studenti e persone in generale. Se hai bisogno di ulteriore aiuto o chiarimenti, non esitare a scrivere la tua richiesta in un commento qui sotto o via email. Cercheremo di aiutarti! Buona fortuna!
Tags: Coseno, Cotangente, Esempio, Funzioni, Seno, Tangente, Trigonometriche

 Attendere prego...
Attendere prego...